Question

（本小题满分12分）

三棱锥中，，,

（1） 求证：面面

（2） 求二面角的余弦值．

Answer 1

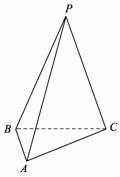（1） 证明：取BC中点O，连接AO，PO，由已知△BAC为直角三角形，

所以可得OA=OB=OC，又知PA=PB=PC，

则△POA≌△POB≌△POC………………………………2分

∴∠POA=∠POB=∠POC=90°，∴PO⊥OB,PO⊥OA,OB∩OA=O

所以PO⊥面BCD，…………………………………………………………………… 4分

面ABC，∴面PBC⊥面ABC………………………5分

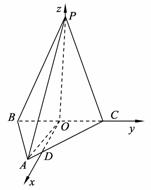
（2） 解：过O作OD与BC垂直，交AC于D点，

如图建立坐标系O—xyz

则，，，，

…………………7分

设面PAB的法向量为n₁=(x,y,z)，由n₁· =0，n₁·=0,可知n₁=(1,-,1)

同理可求得面PAC的法向量为n₁=(3,,1)………………………………………10分

cos(n₁, n₂)==……………………………………………………………12分