题目内容
已知数列{an}的前n项和为Sn,且a1=2, .从{an}中抽出部分项
.从{an}中抽出部分项 ,(k1<k2<…<kn<…)组成的数列
,(k1<k2<…<kn<…)组成的数列 是等比数列,设该等比数列的公比为q,其中
是等比数列,设该等比数列的公比为q,其中 .
.
(1)求a2的值;
(2)当q取最小时,求{kn}的通项公式;
(3)求k1+k2+…+kn的值.
解:(1)令n=1得 ,即
,即 ,
,
又a1=2,∴ .
.
(2)当n≥2时,由 ?nan+1-(n-1)an=an+
?nan+1-(n-1)an=an+ n
n ,由(1)可知:
,由(1)可知: .
.
∴?n∈N*,都有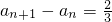 .
.
∴数列{an}是以2为首项, 为公差的等差数列,∴
为公差的等差数列,∴ .
.
解法一:数列{an}是正项递增等差数列,故数列 的公比q>1,
的公比q>1,
若k2=2,则由 ,得
,得 ,此时
,此时 ,由
,由 解得
解得 ,所以k2>2,同理k2>3;
,所以k2>2,同理k2>3;
若k2=4,则由a4=4得q=2,此时 组成等比数列,
组成等比数列,
∴ ,3•2n-1=m+2,对任何正整数n,只要取m=3•2n-1-2,即
,3•2n-1=m+2,对任何正整数n,只要取m=3•2n-1-2,即 是数列{an}的第3•2n-1-2项.最小的公比q=2.
是数列{an}的第3•2n-1-2项.最小的公比q=2.
∴ .
.
解法二:数列{an}是正项递增等差数列,故数列 的公比q>1,
的公比q>1,
设存在 (k1<k2<…<kn<…)组成的数列
(k1<k2<…<kn<…)组成的数列 是等比数列,
是等比数列,
则 ,即
,即
∵k2、k3∈N*且k2>1所以k2+2必有因数3,即可设k2+2=3t,t≥2,t∈N,
当数列 的公比q最小时,即k2=4,?q=2最小的公比q=2.∴
的公比q最小时,即k2=4,?q=2最小的公比q=2.∴ .
.
(3)由(2)可得从{an}中抽出部分项 (k1<k2<…<kn<…)组成的数列
(k1<k2<…<kn<…)组成的数列 是等比数列,其中k1=1,
是等比数列,其中k1=1,
那么 的公比是
的公比是 ,其中由解法二可得k2=3t-2,t≥2,t∈N.
,其中由解法二可得k2=3t-2,t≥2,t∈N.



 ,t≥2,t∈N
,t≥2,t∈N
所以 .
.
分析:(1)由已知:a1=2, .令n=1即可得出;
.令n=1即可得出;
(2)当n≥2时,由 ?nan+1-(n-1)an=an+
?nan+1-(n-1)an=an+ n
n ,(n=1时也成立)即可得出通项an.
,(n=1时也成立)即可得出通项an.
解法一:数列{an}是正项递增等差数列,故数列 的公比q>1,由k2=2,3,经验证不符合题意,应舍去;若k2=4,则由a4=4得q=2,此时
的公比q>1,由k2=2,3,经验证不符合题意,应舍去;若k2=4,则由a4=4得q=2,此时 组成等比数列,可求出kn;
组成等比数列,可求出kn;
解法二:设存在 (k1<k2<…<kn<…)组成的数列
(k1<k2<…<kn<…)组成的数列 是等比数列,则
是等比数列,则 ,即
,即 即可得出kn.
即可得出kn.
(3)利用(2)求出的kn,利用等比数列的前n项和公式即可得出.
点评:熟练掌握数列的通项与前n项和公式Sn之间的关系 ,等差数列与等比数列的通项公式及其前n项和公式事件他的关键.
,等差数列与等比数列的通项公式及其前n项和公式事件他的关键.
 ,即
,即 ,
,又a1=2,∴
 .
.(2)当n≥2时,由
 ?nan+1-(n-1)an=an+
?nan+1-(n-1)an=an+ n
n ,由(1)可知:
,由(1)可知: .
.∴?n∈N*,都有
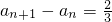 .
.∴数列{an}是以2为首项,
 为公差的等差数列,∴
为公差的等差数列,∴ .
.解法一:数列{an}是正项递增等差数列,故数列
 的公比q>1,
的公比q>1,若k2=2,则由
 ,得
,得 ,此时
,此时 ,由
,由 解得
解得 ,所以k2>2,同理k2>3;
,所以k2>2,同理k2>3;若k2=4,则由a4=4得q=2,此时
 组成等比数列,
组成等比数列,∴
 ,3•2n-1=m+2,对任何正整数n,只要取m=3•2n-1-2,即
,3•2n-1=m+2,对任何正整数n,只要取m=3•2n-1-2,即 是数列{an}的第3•2n-1-2项.最小的公比q=2.
是数列{an}的第3•2n-1-2项.最小的公比q=2.∴
 .
.解法二:数列{an}是正项递增等差数列,故数列
 的公比q>1,
的公比q>1,设存在
 (k1<k2<…<kn<…)组成的数列
(k1<k2<…<kn<…)组成的数列 是等比数列,
是等比数列,则
 ,即
,即
∵k2、k3∈N*且k2>1所以k2+2必有因数3,即可设k2+2=3t,t≥2,t∈N,
当数列
 的公比q最小时,即k2=4,?q=2最小的公比q=2.∴
的公比q最小时,即k2=4,?q=2最小的公比q=2.∴ .
.(3)由(2)可得从{an}中抽出部分项
 (k1<k2<…<kn<…)组成的数列
(k1<k2<…<kn<…)组成的数列 是等比数列,其中k1=1,
是等比数列,其中k1=1,那么
 的公比是
的公比是 ,其中由解法二可得k2=3t-2,t≥2,t∈N.
,其中由解法二可得k2=3t-2,t≥2,t∈N.


 ,t≥2,t∈N
,t≥2,t∈N所以
 .
.分析:(1)由已知:a1=2,
 .令n=1即可得出;
.令n=1即可得出;(2)当n≥2时,由
 ?nan+1-(n-1)an=an+
?nan+1-(n-1)an=an+ n
n ,(n=1时也成立)即可得出通项an.
,(n=1时也成立)即可得出通项an.解法一:数列{an}是正项递增等差数列,故数列
 的公比q>1,由k2=2,3,经验证不符合题意,应舍去;若k2=4,则由a4=4得q=2,此时
的公比q>1,由k2=2,3,经验证不符合题意,应舍去;若k2=4,则由a4=4得q=2,此时 组成等比数列,可求出kn;
组成等比数列,可求出kn;解法二:设存在
 (k1<k2<…<kn<…)组成的数列
(k1<k2<…<kn<…)组成的数列 是等比数列,则
是等比数列,则 ,即
,即 即可得出kn.
即可得出kn.(3)利用(2)求出的kn,利用等比数列的前n项和公式即可得出.
点评:熟练掌握数列的通项与前n项和公式Sn之间的关系
 ,等差数列与等比数列的通项公式及其前n项和公式事件他的关键.
,等差数列与等比数列的通项公式及其前n项和公式事件他的关键. 
练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |