题目内容
经过点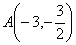 ,倾斜角为
,倾斜角为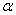 的直线
的直线 ,与曲线
,与曲线 :
: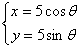 (
(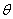 为参数)相交于
为参数)相交于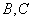 两点.
两点.
(1)写出直线 的参数方程,并求当
的参数方程,并求当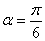 时弦
时弦 的长;
的长;
(2)当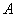 恰为
恰为 的中点时,求直线
的中点时,求直线 的方程;
的方程;
(3)当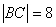 时,求直线
时,求直线 的方程;
的方程;
(4)当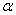 变化时,求弦
变化时,求弦 的中点的轨迹方程.
的中点的轨迹方程.
(1)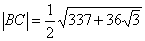 ;(2)
;(2) ;(3)
;(3) 或
或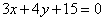
(4)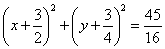
【解析】
试题分析:(1)将参数方程转化为直角坐标系下的普通方程;掌握常见的将参数方程转化为直角坐标系下的普通方程;(2)解决直线和曲线的综合问题:第一步:根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步:联立方程:把所设直线方程与曲线的方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式 :计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论.(4)根据题意设点根据点到直线的距离公式.
:计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论.(4)根据题意设点根据点到直线的距离公式.
试题解析:解:(1) 的参数方程
的参数方程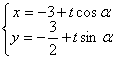 (
( 为参数). 1分
为参数). 1分
曲线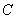 化为:
化为: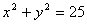 ,将直线参数方程的
,将直线参数方程的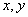 代入,得
代入,得
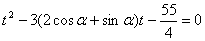
∵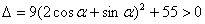 恒成立, 3分
恒成立, 3分
∴方程必有相异两实根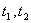 ,且
,且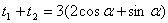 ,
,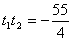 .
.
∴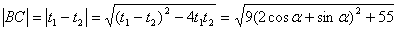
∴当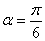 时,
时,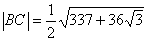 . 5分
. 5分
(2)由 为
为 中点,可知
中点,可知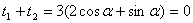 ,
,
∴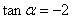 ,
,
故直线 的方程为
的方程为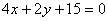 . 7分
. 7分
(3)∵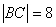 ,得
,得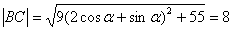
∴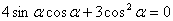 ,
,
∴ 或
或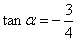
故直线 的方程为
的方程为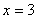 或
或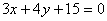 9分
9分
(4)∵ 中点对应参数
中点对应参数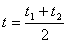
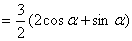
∴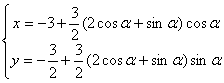 ( 参数
( 参数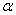
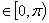 ),消去
),消去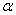 ,得
,得
弦 的中点的轨迹方程为
的中点的轨迹方程为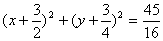 ;
;
轨迹是以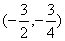 为圆心,
为圆心,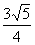 为半径的圆. 10分
为半径的圆. 10分
考点:(1)求弦长问题;(2)求直线方程;(3)中点弦的轨迹方程.

练习册系列答案
相关题目
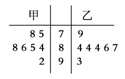 青年歌手大奖赛共有10名选手参赛,并请了7名评委.如图所示的茎叶图是7名评委给参加最后决赛的两位选手甲、乙评定的成绩,去掉一个最高分和一个最低分后,甲、乙选手剩余数据的平均成绩分别为________、________.
青年歌手大奖赛共有10名选手参赛,并请了7名评委.如图所示的茎叶图是7名评委给参加最后决赛的两位选手甲、乙评定的成绩,去掉一个最高分和一个最低分后,甲、乙选手剩余数据的平均成绩分别为________、________.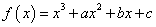 ,在定义域
,在定义域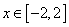 上表示的曲线过原点,且在
上表示的曲线过原点,且在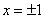 处的切线斜率均为
处的切线斜率均为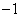 .有以下命题:
.有以下命题: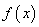 是奇函数;②若
是奇函数;②若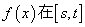 内递减,则
内递减,则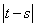 的最大值为4;③
的最大值为4;③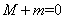 ;④若对
;④若对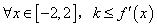 恒成立,则
恒成立,则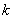 的最大值为2.其中正确命题的个数为 ( )
的最大值为2.其中正确命题的个数为 ( ) 的圆心坐标是( )
的圆心坐标是( ) B.
B. C.
C. D.
D.
 ,
, ,
, 所围成的图形面积为 .
所围成的图形面积为 . )2 D.y=x,y=
)2 D.y=x,y=
 ))的值为( )
))的值为( ) B.-
B.- 中,
中, 成等差数列,则
成等差数列,则 ( )
( )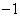 或3 D.1或27
或3 D.1或27