题目内容
已知|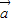 |=1,|
|=1,|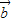 |=2,
|=2,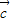 =2
=2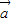 +3
+3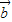 ,
,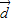 =14
=14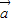 -5
-5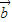 ,若
,若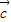 ⊥
⊥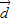 ,则
,则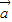 与
与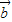 的夹角为( )
的夹角为( )A.30°
B.60°
C.120°
D.150°
【答案】分析:设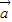 与
与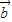 的夹角为θ,则由两个向量的数量积的定义求得
的夹角为θ,则由两个向量的数量积的定义求得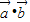 =2cosθ.再由两个向量垂直的性质求得cosθ=
=2cosθ.再由两个向量垂直的性质求得cosθ= ,由此求得θ的值.
,由此求得θ的值.
解答:解:设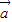 与
与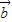 的夹角为θ,则
的夹角为θ,则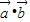 =1×2×cosθ=2cosθ.
=1×2×cosθ=2cosθ.
若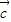 ⊥
⊥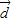 ,则
,则 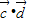 =(2
=(2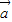 +3
+3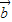 )•(14
)•(14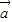 -5
-5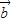 )=28
)=28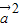 +32
+32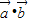 -15
-15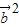 =28+64cosθ-15×4=0,
=28+64cosθ-15×4=0,
解得cosθ= ,∴θ=60°,
,∴θ=60°,
故选B.
点评:本题主要考查两个向量垂直的性质,两个向量坐标形式的运算,两个向量的数量积的定义,属于中档题.
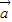 与
与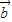 的夹角为θ,则由两个向量的数量积的定义求得
的夹角为θ,则由两个向量的数量积的定义求得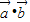 =2cosθ.再由两个向量垂直的性质求得cosθ=
=2cosθ.再由两个向量垂直的性质求得cosθ= ,由此求得θ的值.
,由此求得θ的值.解答:解:设
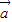 与
与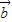 的夹角为θ,则
的夹角为θ,则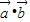 =1×2×cosθ=2cosθ.
=1×2×cosθ=2cosθ.若
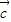 ⊥
⊥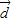 ,则
,则 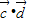 =(2
=(2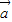 +3
+3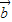 )•(14
)•(14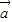 -5
-5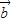 )=28
)=28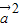 +32
+32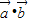 -15
-15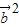 =28+64cosθ-15×4=0,
=28+64cosθ-15×4=0,解得cosθ=
 ,∴θ=60°,
,∴θ=60°,故选B.
点评:本题主要考查两个向量垂直的性质,两个向量坐标形式的运算,两个向量的数量积的定义,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知
(xcosx+3a-b)dx=2a+6,f(t)=
(x3+ax+5a-b)dx为偶函数,则a+b=( )
| ∫ | 1 -1 |
| ∫ | t 0 |
| A、-6 | B、-12 | C、4 | D、-4 |