题目内容
在△ABC中,M是BC的中点,AM=1,点P在AM上且满足 =2
=2 ,
,
则 ·(
·( +
+ )等于( )
)等于( )
A.- | B.- | C. | D. |
A
解析试题分析:因为点P在AM上且满足 =2
=2 ,所以
,所以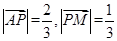 ,所以
,所以 ·(
·( +
+ )=
)=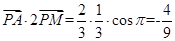 。
。
考点:重心的性质;向量的运算;向量的数量积。
点评: 熟练且灵活掌握向量的平行四边形法则:在△ABC中,M是BC的中点,P为平面上的任意一点,则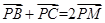 .
.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
已知 和
和 是平面上的两个单位向量,且
是平面上的两个单位向量,且 ,
, ,若O为坐标原点,
,若O为坐标原点, 均为正常数,则
均为正常数,则 的最大值为 ( )
的最大值为 ( )
A. | B. | C. | D. |
若平面向量 满足
满足 =
= ,
, ,
, ,则平面向量
,则平面向量 的夹角为( )
的夹角为( )
A. | B. | C. | D. |
已知点 是
是 重心 ,若
重心 ,若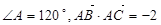 , 则
, 则 的最小值是( )
的最小值是( )
A.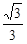 | B. | C. | D. |
 为正方形,
为正方形, 平面
平面 ,
, ,则
,则 与
与 所成角的度数为
所成角的度数为
| A.30° | B.45° | C.60° | D.90° |
在 中,
中, 为边
为边 中线
中线 上的一点,若
上的一点,若 ,则
,则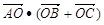 的( )
的( )
| A.最大值为8 | B.最大值为4 | C.最小值-4 | D.最小值为-8 |
 ,那么在图②中所示的平行六面体
,那么在图②中所示的平行六面体 中,
中, 等于( )
等于( )




 的直线与两坐标轴的正半轴交于
的直线与两坐标轴的正半轴交于 、
、 两点,
两点, 为坐标原点,
为坐标原点, ,则四边形
,则四边形 周长的最小值等于
周长的最小值等于



