题目内容

已知抛物线y²=2px（p＞0），且准线与y轴的距离为2．
（1）求此抛物线的方程；
（2）点P为抛物线上一点，且其纵坐标为 $数学公式$ ，求点P到抛物线焦点的距离．

解：（1）因为抛物线准线与y轴的距离为2，
所以p=4，…（3分）
抛物线的方程为y²=8x．…（6分）
（2）设 $\text{[math]}$ ，则8=8x₀，
所以x₀=1，…（9分）
所以点P到抛物线焦点的距离为 $\text{[math]}$ ．…（12分）
分析：（1）利用抛物线的简单性质得出：抛物线准线与y轴的距离为 $\text{[math]}$ ，所以p=4最后写出抛物线的方程即可；
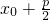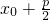（2）先设 $\text{[math]}$ ，将其代入抛物线的方程，求出x₀=1，再利用抛物线的定义得到点P到抛物线焦点的距离为 $\text{[math]}$ 即可．
点评：本小题主要考查抛物线的标准方程、抛物线的简单性质等基础知识，考查运算求解能力，考查数形结合思想．属于基础题．

练习册系列答案

暑假作业长春出版社系列答案

智慧鸟快乐衔接辅导专家系列答案

快乐学习报强化训练快乐假期期末复习暑假系列答案

高分装备中考真题分类系列答案

假期作业暑假希望出版社系列答案

练就优等生系列答案

快乐暑假江苏凤凰教育出版社系列答案

假期生活暑假方圆电子音像出版社系列答案

新课堂假期生活暑假用书系列答案

假期作业黄山书社系列答案

相关题目

已知抛物线y²=2px（p＞0）．过动点M（a，0）且斜率为1的直线l与该抛物线交于不同的两点A、B，|AB|≤2p．
（1）求a的取值范围；
（2）若线段AB的垂直平分线交x轴于点N，求△NAB面积的最大值．

已知抛物线y²=2px（p＞0）的焦点为F，准线为l．
（1）求抛物线上任意一点Q到定点N（2p，0）的最近距离；
（2）过点F作一直线与抛物线相交于A，B两点，并在准线l上任取一点M，当M不在x轴上时，证明：

是一个定值，并求出这个值．（其中k_MA，k_MB，k_MF分别表示直线MA，MB，MF的斜率）

已知抛物线y²=2px（p＞0）．过动点M（a，0）且斜率为1的直线l与该抛物线交于不同的两点A、B，|AB|≤2p．求a的取值范围．

（2009•聊城一模）已知抛物线y²=2px（p＞0），过点M（2p，0）的直线与抛物线相交于A，B，

已知抛物线y²=2px（p＞0），M（2p，0），A、B是抛物线上的两点．求证：直线AB经过点M的充要条件是OA⊥OB，其中O是坐标原点．