题目内容
若
，则A∩B=
- A.{（2，1）}
- B.{2，1}
- C.{（2，1），（0，1）}
- D.{x，y|x=2，y=1}
A
分析：集合A中的函数，当x大于0时，y=1；当x小于0时，y=-1；集合B为y=x-1图象上的点构成，画出相应的图形，如图所示，由图象可得出两函数的交点坐标，即为A与B的交集．
解答：
解：集合A中的y=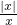
，当x＞0时，|x|=x，y=1；当x＜0时，|x|=-x，y=-1，
集合B为函数y=x-1上的点构成，
画出相应的图形，
由图形可得出A∩B={（2，1）}．
故选A
点评：此题考查了交集及其运算，利用了数形结合的思想，熟练掌握交集的定义是解本题的关键．
分析：集合A中的函数，当x大于0时，y=1；当x小于0时，y=-1；集合B为y=x-1图象上的点构成，画出相应的图形，如图所示，由图象可得出两函数的交点坐标，即为A与B的交集．
解答：
解：集合A中的y=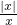，当x＞0时，|x|=x，y=1；当x＜0时，|x|=-x，y=-1，集合B为函数y=x-1上的点构成，
画出相应的图形，
由图形可得出A∩B={（2，1）}．
故选A
点评：此题考查了交集及其运算，利用了数形结合的思想，熟练掌握交集的定义是解本题的关键．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
下列命题中：
①若a与b互为相反向量，则a+b=0；
②若k为实数，且k•a=0，则a=0或k=0；
③若a•b=0，则a=0或b=0；
④若a与b为平行的向量，则a•b=|a||b|；
⑤若|a|=1，则a=±1．
其中假命题的个数为（ ）
①若a与b互为相反向量，则a+b=0；
②若k为实数，且k•a=0，则a=0或k=0；
③若a•b=0，则a=0或b=0；
④若a与b为平行的向量，则a•b=|a||b|；
⑤若|a|=1，则a=±1．
其中假命题的个数为（ ）
| A、5个 | B、4个 | C、3个 | D、2个 |
命题“若a，b都是奇数，则a+b是偶数”的逆否命题是（ ）
| A、若a，b都不是奇数，则a+b是偶数 | B、若a+b是偶数，则a，b都是奇数 | C、若a+b不是偶数，则a，b都不是奇数 | D、若a+b不是偶数，则a，b不都是奇数 |