题目内容
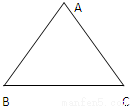
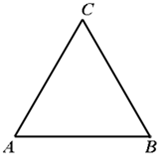 如图,△ABC为一个等腰三角形形状的空地,腰CA的长为3(百米),底AB的长为4(百米).现决定在空地内筑一条笔直的小路EF(宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等、面积分别为S1和S2.
如图,△ABC为一个等腰三角形形状的空地,腰CA的长为3(百米),底AB的长为4(百米).现决定在空地内筑一条笔直的小路EF(宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等、面积分别为S1和S2.(1)若小路一端E为AC的中点,求此时小路的长度;
(2)求
| S1 | S2 |
分析:(1)根据题意可知F不在BC上,根据余弦定理求出cosA的值,然后根据余弦定理求出EF的长即可;
(2)若E、F分别在AC和AB上,设AE=x,AF=y,然后利用三角形的面积公式求出S2和S1=S三角形ABC-S2=,再根据基本不等式求出比值的最值即可,若E、F分别在AC和BC上,设CE=x,CF=y,同上根据基本不等式求出比值的最值即可.
(2)若E、F分别在AC和AB上,设AE=x,AF=y,然后利用三角形的面积公式求出S2和S1=S三角形ABC-S2=,再根据基本不等式求出比值的最值即可,若E、F分别在AC和BC上,设CE=x,CF=y,同上根据基本不等式求出比值的最值即可.
解答:解:(1)因为:AE=CE=
AE+4>CE+3 所以F不在BC上,
AE+AF+EF=CE+CB+FB+EF
所以AE=CE AF=CB+BF 4-BF=BF+3 BF=
cosA=
=
所以EF2=AE2+AF2-2AE×AF×cosA=
所以EF=
E为AC中点时,此时小路的长度为
(2)若E、F分别在AC和AB上,
sinA=
设AE=x,AF=y,
所以S2=
xysinA=
S1=S三角形ABC-S2=2
-S2
因为x+y=3-x+4-y+3
所以x+y=5
=
≥
-1
xy≤(
)2 =
当且仅当x=y=
时取等号
所以
=
当且仅当x=y=
时取等号
最小值是
若E、F分别在AC和BC上,
=
sinC=
设CE=x,CF=y
同上可得
≥
当且仅当x=y=
取等号
若E、F分别在AC和BC上,最小值是
| 3 |
| 2 |
AE+AF+EF=CE+CB+FB+EF
所以AE=CE AF=CB+BF 4-BF=BF+3 BF=
| 1 |
| 2 |
cosA=
| AC2+AB2-BC2 |
| 2AC×AB |
| 2 |
| 3 |
所以EF2=AE2+AF2-2AE×AF×cosA=
| 15 |
| 2 |
所以EF=
| ||
| 2 |
E为AC中点时,此时小路的长度为
| ||
| 2 |
(2)若E、F分别在AC和AB上,
sinA=
| ||
| 3 |
设AE=x,AF=y,
所以S2=
| 1 |
| 2 |
| ||
| 6 |
S1=S三角形ABC-S2=2
| 5 |
因为x+y=3-x+4-y+3
所以x+y=5
| S1 |
| S2 |
2
| ||||
|
| 48 |
| 25 |
xy≤(
| x+y |
| 2 |
| 25 |
| 4 |
当且仅当x=y=
| 5 |
| 2 |
所以
| S1 |
| S2 |
| 23 |
| 25 |
当且仅当x=y=
| 5 |
| 2 |
最小值是
| 23 |
| 25 |
若E、F分别在AC和BC上,
| c |
| sinC |
| a |
| sinA |
4
| ||
| 9 |
设CE=x,CF=y
同上可得
| S1 |
| S2 |
| 11 |
| 25 |
当且仅当x=y=
| 5 |
| 2 |
若E、F分别在AC和BC上,最小值是
| 11 |
| 25 |
点评:本题主要考查了解三角形的实际应用,以及利用基本不等式求最值问题,同时考查了分类讨论的思想,属于中档题.

练习册系列答案
相关题目
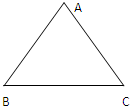 (2011•江西模拟)如图,△ABC为一个等腰三角形的空地,底边AB长为4(百米),腰长为3(百米),现决定在空地上修一条笔直的小路EF(宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形周长相等,面积分别为S1和S2,
(2011•江西模拟)如图,△ABC为一个等腰三角形的空地,底边AB长为4(百米),腰长为3(百米),现决定在空地上修一条笔直的小路EF(宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形周长相等,面积分别为S1和S2,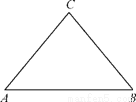
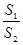 的最小值.
的最小值.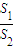 的最小值.
的最小值.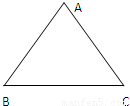
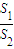 的最小值.
的最小值.