题目内容
 如图,B、C分别为
如图,B、C分别为 =1(a>b>0)的顶点与焦点,若∠ABC=90°,则该椭圆的离心率为
=1(a>b>0)的顶点与焦点,若∠ABC=90°,则该椭圆的离心率为
- A.

- B.1-

- C.
 -1
-1 - D.

A
分析:由题意知|AC|2=|AB|2+|BC|2,即(a+c)2=a2+2b2+c2,由此可以推导出该椭圆的离心率.
解答:|AB|2=a2+b2,|BC|2=b2+c2,
|AC|2=(a+c)2.
∵∠ABC=90°,
∴|AC|2=|AB|2+|BC|2,即(a+c)2=a2+2b2+c2,
∴2ac=2b2,即b2=aC、
∴a2-c2=aC、
∴ -
- =1,即
=1,即 -e=1.
-e=1.
解之得e=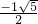 ,又∵e>0,
,又∵e>0,
∴e= .
.
故选A.
点评:本题考查椭圆的基本性质,解题时结合图形效果较好.
分析:由题意知|AC|2=|AB|2+|BC|2,即(a+c)2=a2+2b2+c2,由此可以推导出该椭圆的离心率.
解答:|AB|2=a2+b2,|BC|2=b2+c2,
|AC|2=(a+c)2.
∵∠ABC=90°,
∴|AC|2=|AB|2+|BC|2,即(a+c)2=a2+2b2+c2,
∴2ac=2b2,即b2=aC、
∴a2-c2=aC、
∴
 -
- =1,即
=1,即 -e=1.
-e=1.解之得e=
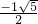 ,又∵e>0,
,又∵e>0,∴e=
 .
.故选A.
点评:本题考查椭圆的基本性质,解题时结合图形效果较好.

练习册系列答案
相关题目
 18、如图,E、F分别为直角三角形ABC的直角边AC和斜边AB的中点,沿EF将△AEF折起到△A′EF的位置,连接A′B、A′C,P为A′C的中点.
18、如图,E、F分别为直角三角形ABC的直角边AC和斜边AB的中点,沿EF将△AEF折起到△A′EF的位置,连接A′B、A′C,P为A′C的中点. 如图,M是单位圆与x轴正半轴的交点,点P在单位圆上,
如图,M是单位圆与x轴正半轴的交点,点P在单位圆上,
 =1(a>b>0)的顶点与焦点,若∠ABC=90°,则该椭圆的离心率为( )
=1(a>b>0)的顶点与焦点,若∠ABC=90°,则该椭圆的离心率为( )


 -1
-1