题目内容
(本小题满分13分)
已知函数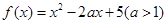 .
.
(1) 若函数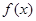 的定义域和值域均为
的定义域和值域均为 ,求实数
,求实数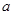 的值;
的值;
(2) 若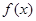 在区间
在区间 上是减函数,且对任意的
上是减函数,且对任意的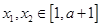 ,
,
总有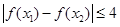 ,求实数
,求实数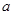 的取值范围;
的取值范围;
(3) 若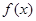 在
在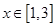 上有零点,求实数
上有零点,求实数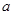 的取值范围.
的取值范围.
【答案】
(1)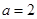 ;(2)
;(2)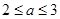 ;(3)
;(3)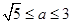 。
。
【解析】本试题主要是考查了函数的定义域和值域以及函数单调性以及函数零点的综合运用。
(1)因为函数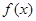 的定义域和值域均为
的定义域和值域均为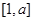 ,而
,而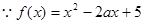 在
在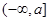 上的减函数
上的减函数

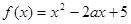 在
在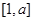 上单调递减,得到参数a的值
上单调递减,得到参数a的值
(2)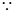
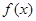 在区间
在区间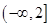 上是减函数,
上是减函数,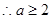
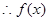 在
在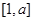 上单调递减,在
上单调递减,在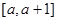 上单调递,然后分析对任意的
上单调递,然后分析对任意的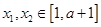 ,总有
,总有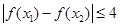
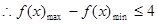 ,得到结论。
,得到结论。
(3)
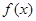 在
在 上有零点,
上有零点,
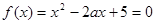 在
在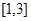 上有解。
上有解。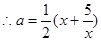 在
在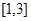 上有解,得到参数a的范围。
上有解,得到参数a的范围。
解:(1)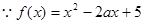 在
在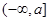 上的减函数,
上的减函数,

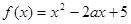 在
在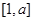 上单调递减
上单调递减
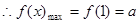 且
且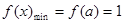 ………………………………2分
………………………………2分
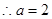 ……………………………………………………………………4分
……………………………………………………………………4分
(2)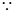
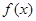 在区间
在区间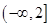 上是减函数,
上是减函数,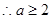
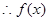 在
在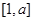 上单调递减,在
上单调递减,在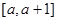 上单调递增
上单调递增
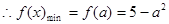 ,
,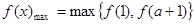 ………6分
………6分
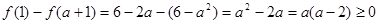
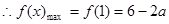
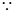 对任意的
对任意的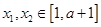 ,总有
,总有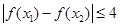
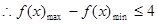 ,……………………………………………………8分
,……………………………………………………8分
即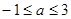 又
又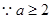 ,
,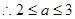 ………………………………………9分
………………………………………9分
(3)
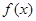 在
在 上有零点,
上有零点,
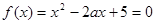 在
在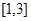 上有解。
上有解。
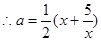 在
在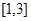 上有解……………………………………………11分
上有解……………………………………………11分
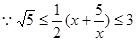
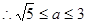 ……………………………………13分
……………………………………13分

练习册系列答案
相关题目

 .
. 的最小正周期和最大值;
的最小正周期和最大值; 在区间
在区间 上的图象.
上的图象. ,且方程
,且方程 有两个不同的实数根,求实数m的取值范围.
有两个不同的实数根,求实数m的取值范围. 的函数
的函数 是奇函数.
是奇函数. 的值;(2)判断函数
的值;(2)判断函数 的单调性;
的单调性; ,不等式恒成立
,不等式恒成立 ,求k的取值范围.
,求k的取值范围. ,
,  ,
, .
. (∁
(∁ ; (2)若
; (2)若 ,求
,求 的取值范围.
的取值范围. 的所有棱长都为2,
的所有棱长都为2, 为
为 的中点。
的中点。 ∥平面
∥平面 ;
; 所成的角。www.7caiedu.cn
所成的角。www.7caiedu.cn

 为锐角,且
为锐角,且 ,函数
,函数 ,数列{
,数列{ }的首项
}的首项 .
. 的表达式;
的表达式; 中,若
中,若 A=2
A=2 ,BC=2,求
,BC=2,求 的前
的前 项和
项和