题目内容
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)两相邻对称轴间的距离为 ,且图象的一个最低点为
,且图象的一个最低点为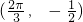 .
.
(1)求f(x)的解析式;
(2)求函数f(x)的单调增区间与对称轴;
(3)当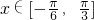 时,求函数f(x)的值域.
时,求函数f(x)的值域.
解:(1)由题意知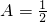 ,
,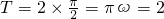
又图象有一个最低点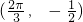 ,
,
∴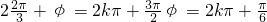
而0<φ<π,
∴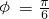 ,
,
故 ;
;
(2)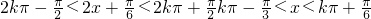 ;
;

∴f(x)的增区间是 ,
,
对称轴为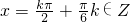 ;
;
(3)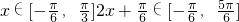 ,
,
∴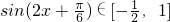 ,
,
∴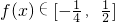 .
.
分析:(1)由已知中函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)两相邻对称轴间的距离为 ,我们可以确定函数的周期,进而求出ω值,再根据图象的一个最低点为
,我们可以确定函数的周期,进而求出ω值,再根据图象的一个最低点为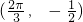 ,可以结合A>0,0<φ<π求出A值及φ值,进而得到f(x)的解析式;
,可以结合A>0,0<φ<π求出A值及φ值,进而得到f(x)的解析式;
(2)根据(1)中正弦型函数的解析式,结合正弦型函数的单调性,我们可以构造一个关于x的不等式 ,解不等式求出x的范围,即可得到函数f(x)的单调增区间,根据正弦函数的对称性,可以得到函数的对称轴方程.
,解不等式求出x的范围,即可得到函数f(x)的单调增区间,根据正弦函数的对称性,可以得到函数的对称轴方程.
(3)根据(2)结论,我们易判断函数f(x)在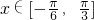 时的单调性,进而得到函数f(x)的值域.
时的单调性,进而得到函数f(x)的值域.
点评:本题考查的知识点是正弦型函数的解析式的求法,正弦型函数的值域,正弦型函数的单调性,正弦型函数的对称性,其中根据已知条件求出函数的解析式是解答本题的关键.
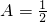 ,
,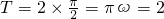
又图象有一个最低点
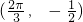 ,
,∴
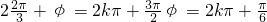
而0<φ<π,
∴
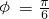 ,
,故
 ;
;(2)
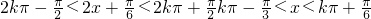 ;
;
∴f(x)的增区间是
 ,
,对称轴为
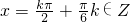 ;
;(3)
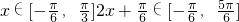 ,
,∴
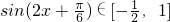 ,
,∴
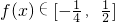 .
.分析:(1)由已知中函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)两相邻对称轴间的距离为
 ,我们可以确定函数的周期,进而求出ω值,再根据图象的一个最低点为
,我们可以确定函数的周期,进而求出ω值,再根据图象的一个最低点为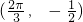 ,可以结合A>0,0<φ<π求出A值及φ值,进而得到f(x)的解析式;
,可以结合A>0,0<φ<π求出A值及φ值,进而得到f(x)的解析式;(2)根据(1)中正弦型函数的解析式,结合正弦型函数的单调性,我们可以构造一个关于x的不等式
 ,解不等式求出x的范围,即可得到函数f(x)的单调增区间,根据正弦函数的对称性,可以得到函数的对称轴方程.
,解不等式求出x的范围,即可得到函数f(x)的单调增区间,根据正弦函数的对称性,可以得到函数的对称轴方程.(3)根据(2)结论,我们易判断函数f(x)在
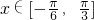 时的单调性,进而得到函数f(x)的值域.
时的单调性,进而得到函数f(x)的值域.点评:本题考查的知识点是正弦型函数的解析式的求法,正弦型函数的值域,正弦型函数的单调性,正弦型函数的对称性,其中根据已知条件求出函数的解析式是解答本题的关键.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目