题目内容
若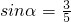
，
，则
=
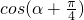- A.
- B.
- C.
- D.
C
分析：由sinα的值大于0，且α的范围，可得出α的具体范围，然后根据同角三角函数间的基本关系求出cosα，最后利用两角和的余弦函数公式及特殊角的三角函数值化简，把sinα和cosα的值代入可得出值．
解答：∵sinα=
＞0，，
∴
，且
，
则
．
故选C
点评：此题考查了同角三角函数间的基本关系，特殊角的三角函数值以及两角和与差的余弦函数公式，由sinα的值大于0且α的范围，得出α的具体范围是本题的突破点．
分析：由sinα的值大于0，且α的范围，可得出α的具体范围，然后根据同角三角函数间的基本关系求出cosα，最后利用两角和的余弦函数公式及特殊角的三角函数值化简，把sinα和cosα的值代入可得出值．
解答：∵sinα=
＞0，，∴
，且，则
．故选C
点评：此题考查了同角三角函数间的基本关系，特殊角的三角函数值以及两角和与差的余弦函数公式，由sinα的值大于0且α的范围，得出α的具体范围是本题的突破点．
练习册系列答案
相关题目
=3，则
≥3”，的否命题是
、
、
表示三条不同的直线，
表示平面，给出下列命题：
中，角
所对的边分别为
，若
，
，则
( )
(B)
(C)
(D)
,
，则
}
B. {
}
}
D. {
}
=3，则
≥3”的否命题是（ ）