题目内容
（本小题满分12分）
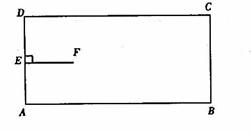
如图为机器人踢球的场地，
，机器人先从AD中点E进入场地到点F处，
，场地内有一小球从点B向点A运动，与此同时机器人从点F出发去截小球，机器人与小球均作匀速直线运动，并且小球运动速度是机器人行走速度的2倍，若忽略机器人原地旋转所需的时间，则机器人最快可在何处截住小球？
（本小题满分12分）
设机器人最快在P点截住小球，则
，作
于
则
=-
=-
， 
4分
化简为
，
，8分
或
，此时
，
，所以机器人最快在
边上距离
70cm处截住小球。 12分
法二:设机器人在AB上P处截住小球，设
，则
，解得
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
