题目内容
附加题:若函数f(x)=log2(kx2+4kx+3)的定义域为R,求k的取值范围.
分析:由已知函数的定义域为R可得,kx2+4kx+3>0恒成立,当k=0时,3>0,恒成立,故k=0满足条件,当k≠0时,则
,解不等式可求k的范围.
|
解答:解:由已知函数的定义域为R可得,kx2+4kx+3>0恒成立
当k=0时,3>0,恒成立,故k=0满足条件
当k≠0时,则
∴0<k<
综上可得,0≤k<
.
当k=0时,3>0,恒成立,故k=0满足条件
当k≠0时,则
|
∴0<k<
| 3 |
| 4 |
综上可得,0≤k<
| 3 |
| 4 |
点评:本题以对数函数的定义域的恒成立为切入点,主要考查了二次函数的恒成立,注意对二次项系数k的讨论是解答本题中的难点.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
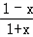 ,其中a>0.
,其中a>0.