题目内容
B.选修4—2 矩阵与变换
已知矩阵
 ,其中
,其中 ,若点
,若点 在矩阵
在矩阵 的变换下得到点
的变换下得到点 ,
,
(1)求实数a的值;
(2)求矩阵 的特征值及其对应的特征向量.
的特征值及其对应的特征向量.
【答案】
解:(1)由
 =
= ,(2分) ∴
,(2分) ∴ . (3分)
. (3分)
(2)由(1)知
 ,则矩阵
,则矩阵 的特征多项式为
的特征多项式为
 (5分)
(5分)
令 ,得矩阵
,得矩阵 的特征值为
的特征值为 与4. (6分)
与4. (6分)
当 时,
时, 
∴矩阵 的属于特征值
的属于特征值 的一个特征向量为
的一个特征向量为 ; (8分)
; (8分)
当 时,
时, 
∴矩阵 的属于特征值
的属于特征值 的一个特征向量为
的一个特征向量为 . (10分)
. (10分)
【解析】略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
从A,B,C,D四个中选做2个,每题10分,共20分
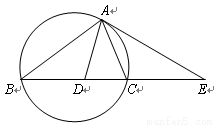
| A.选修4—1 几何证明选讲 如图,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与BC交于点D。求证:  。 。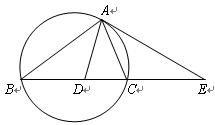 |
| B.选修4—2 矩阵与变换 在平面直角坐标系 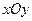 中,设椭圆 中,设椭圆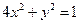 在矩阵对应的变换作用下得到曲线F,求F的方程。 在矩阵对应的变换作用下得到曲线F,求F的方程。 |
| C.选修4—4 参数方程与极坐标 在平面直角坐标系 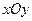 中,点 中,点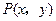 是椭圆 是椭圆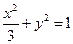 上的一个动点,求 上的一个动点,求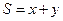 的最大值。 的最大值。 |
| D.选修4—5 不等式证明选讲 |
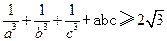 。
。  【选做题】在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.请在答题卡指定区域内作答.解答应写出文字说明、证明过程或演算步骤.
【选做题】在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.请在答题卡指定区域内作答.解答应写出文字说明、证明过程或演算步骤.

 ,其中
,其中 ,若点
,若点 在矩阵
在矩阵 ,
,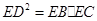 。
。
 中,设椭圆
中,设椭圆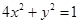 在矩阵对应的变换作用下得到曲线F,求F的方程。
在矩阵对应的变换作用下得到曲线F,求F的方程。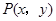 是椭圆
是椭圆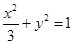 上的一个动点,求
上的一个动点,求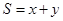 的最大值。
的最大值。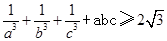 。
。