题目内容
如图,已知四棱锥S—ABCD的底面是边长为4的正方形,S在底面的射影O在正方形ABCD内,且O到AB,AD的距离分别为2和1.
(1)求证:![]() ·
·![]() 是定值;
是定值;
(2)已知P是SC的中点,且SO=3,问在棱SA上是否存在一点Q,使异面直线OP与BQ所成的角为90°?若存在,请给出证明,并求出AQ的长;若不存在,请说明理由.
解:(1)在△SDC内,作SE⊥CD交CD于E,连结OE.
∵SO⊥平面ABCD,
∴SO⊥CD.
∴CD⊥平面SOE,
∴DE⊥OE.∴OE∥AD.
∴DE=1.从而CE=3.
![]() ·
·![]() =
=![]() ·
·![]() =|
=|![]() ||
||![]() |cos∠SCD=|
|cos∠SCD=|![]() ||
||![]() |=12,
|=12,
∴![]() ·
·![]() 是定值.
是定值.
(2)以O为坐标原点,以OS所在直线为Oz轴,以过O且平行于AD的直线为Ox轴,以过O且平行于AB的直线为Oy轴,建立空间直角坐标系.
则A(2,-1,0),B(2,3,0),C(-2,3,0),S(0,0,3),P(-1,![]() ,
,![]() ),
),
设点Q(x,y,z),则存在λ使![]() =λ
=λ![]() ,
,
即(x-2,y+1,z)=λ(-2,1,3),
得 即
即
令![]() ·
·![]() =(-1,
=(-1,![]() ,
,![]() )·(-2λ,λ-4,3λ)=8λ-6=0,得λ=
)·(-2λ,λ-4,3λ)=8λ-6=0,得λ=![]() .由0<λ<1知,点Q在棱SA上,且Q(
.由0<λ<1知,点Q在棱SA上,且Q(![]() ,-
,-![]() ,
,![]() ),|
),|![]() |=
|=![]() |
|![]() |=
|=![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知四棱锥S-ABCD的底面ABCD是边长为1的正方形,SA⊥平面ABCD,SA=2,E是侧棱SC上的一点.
如图,已知四棱锥S-ABCD的底面ABCD是边长为1的正方形,SA⊥平面ABCD,SA=2,E是侧棱SC上的一点.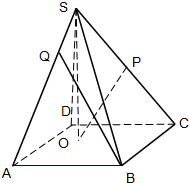 如图,已知四棱锥S-ABCD的底面是边长为4的正方形,S在底面上的射影O落在正方形ABCD内,SO的长为3,O到AB,AD的距离分别为2和1,P是SC的中点.
如图,已知四棱锥S-ABCD的底面是边长为4的正方形,S在底面上的射影O落在正方形ABCD内,SO的长为3,O到AB,AD的距离分别为2和1,P是SC的中点.
 (2008•湖北模拟)如图,已知四棱锥S-ABCD中,△SAD是边长为a的正三角形,平面SAD⊥平面ABCD,四边形ABCD为菱形,∠DAB=60°,P为AD的中点,Q为SB的中点.
(2008•湖北模拟)如图,已知四棱锥S-ABCD中,△SAD是边长为a的正三角形,平面SAD⊥平面ABCD,四边形ABCD为菱形,∠DAB=60°,P为AD的中点,Q为SB的中点. (2010•江西模拟)(如图)已知四棱锥S-ABCD的底面ABCD是菱形,将面SAB,SAD,ABCD 展开成平面后的图形恰好为一正三角形S'SC.
(2010•江西模拟)(如图)已知四棱锥S-ABCD的底面ABCD是菱形,将面SAB,SAD,ABCD 展开成平面后的图形恰好为一正三角形S'SC.