题目内容
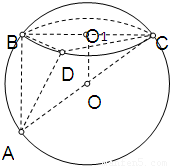
半径为R的球O的截面BCD把球面面积分为两部分,截面圆O1的面积为12π,2OO1=R,BC是截面圆O1的直径,D是圆O1上不同于B,C的一点,CA是球O的一条直径.①求证:平面ADC⊥平面ABD;
②求三棱锥A-BCD的体积最大值;
③当D分BC的两部分的比BD:DC=1:2时,求二面角B-AC-D的正切值.
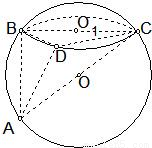
【答案】分析:①证明平面ADC内的直线DC,垂直平面ABD内的两条相交直线AB,BD,即可证明平面ADC⊥平面ABD;
②先求出球的半径,AB=4,要VA-BCD取最大,则需S△BCD取最大即可;
③D分BC的两部分的比BD:DC=1:2,过D作DE⊥BC则DE⊥平面ABC,过D作DF⊥AC于F,连EF,∠EFD为二面角D-AC-B的平面角,解三角形即可求二面角B-AC-D的正切值.
解答:解:(1)连OO1,则OO1⊥面BDC△ABC中,
OO1∥AB
∴AB⊥面BCD,
∵CD在面BCD内
∴AB⊥DC又由题意知BD⊥DC且AB∩BD=B
∴CD⊥面ABD∵CD在面ACD内
∴面ACD⊥面ABD(4分)
(2)∵S⊙=12π∴O1C=2R=2OO1
在△O1OC中OO12+O1C2=R2
∴R=4OO1=2∵AB=2OO1∴AB=4
∵AB⊥面BDC,
要VA-BCD取最大,则需S△BCD取最大
∵(A△BCD)max=
 (9分)
(9分)
(3)当弧BD:弧DC=1:2时∠BO1D=60°,∠DO1C=120°
∴BD= CD=6
CD=6
∵AB⊥面BDC∴面ABC⊥面BDC,面ABC∩面BCD=BC
过D作DE⊥BC则DE⊥平面ABC,过D作DF⊥AC于F,
连EF则∠EFD为二面角D-AC-B的平面角,
在△ADC中,DF=
在△DC中,

∴二面角D-AC-BD的大小为atcsin (14分)
(14分)
点评:本题考查平面与平面垂直的判定,棱柱、棱锥、棱台的体积,二面角及其度量,考查空间想象能力,逻辑思维能力,是中档题.
②先求出球的半径,AB=4,要VA-BCD取最大,则需S△BCD取最大即可;
③D分BC的两部分的比BD:DC=1:2,过D作DE⊥BC则DE⊥平面ABC,过D作DF⊥AC于F,连EF,∠EFD为二面角D-AC-B的平面角,解三角形即可求二面角B-AC-D的正切值.
解答:解:(1)连OO1,则OO1⊥面BDC△ABC中,
OO1∥AB
∴AB⊥面BCD,
∵CD在面BCD内
∴AB⊥DC又由题意知BD⊥DC且AB∩BD=B
∴CD⊥面ABD∵CD在面ACD内
∴面ACD⊥面ABD(4分)
(2)∵S⊙=12π∴O1C=2R=2OO1
在△O1OC中OO12+O1C2=R2
∴R=4OO1=2∵AB=2OO1∴AB=4
∵AB⊥面BDC,
要VA-BCD取最大,则需S△BCD取最大
∵(A△BCD)max=

 (9分)
(9分)(3)当弧BD:弧DC=1:2时∠BO1D=60°,∠DO1C=120°
∴BD=
 CD=6
CD=6∵AB⊥面BDC∴面ABC⊥面BDC,面ABC∩面BCD=BC
过D作DE⊥BC则DE⊥平面ABC,过D作DF⊥AC于F,
连EF则∠EFD为二面角D-AC-B的平面角,
在△ADC中,DF=

在△DC中,


∴二面角D-AC-BD的大小为atcsin
 (14分)
(14分)点评:本题考查平面与平面垂直的判定,棱柱、棱锥、棱台的体积,二面角及其度量,考查空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
相关题目
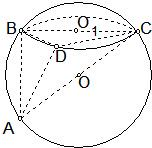 半径为R的球O的截面BCD把球面面积分为两部分,截面圆O1的面积为12π,2OO1=R,BC是截面圆O1的直径,D是圆O1上不同于B,C的一点,CA是球O的一条直径.
半径为R的球O的截面BCD把球面面积分为两部分,截面圆O1的面积为12π,2OO1=R,BC是截面圆O1的直径,D是圆O1上不同于B,C的一点,CA是球O的一条直径. 半径为R的球O的截面BCD把球面面积分为两部分,截面圆O1的面积为12π,2OO1=R,BC是截面圆O1的直径,D是圆O1上不同于B,C的一点,CA是球O的一条直径.
半径为R的球O的截面BCD把球面面积分为两部分,截面圆O1的面积为12π,2OO1=R,BC是截面圆O1的直径,D是圆O1上不同于B,C的一点,CA是球O的一条直径.
 半径为R的球O的截面BCD把球面面积分为两部分,截面圆O1的面积为12π,2OO1=R,BC是截面圆O1的直径,D是圆O1上不同于B,C的一点,CA是球O的一条直径.
半径为R的球O的截面BCD把球面面积分为两部分,截面圆O1的面积为12π,2OO1=R,BC是截面圆O1的直径,D是圆O1上不同于B,C的一点,CA是球O的一条直径. 的两部分的比
的两部分的比 :
: =1:2时,求D点到平面ABC的距离.
=1:2时,求D点到平面ABC的距离.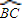 的两部分的比
的两部分的比 :
: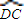 =1:2时,求D点到平面ABC的距离.
=1:2时,求D点到平面ABC的距离.