Question

如图，已知四棱锥P—ABCD，底面ABCD为菱形，PA⊥平面ABCD，∠ABC=60°,E，F分别是BC,PC的中点.

(1)证明：AE⊥PD;

(2)若H为PD上的动点，EH与平面PAD所成最大角的正切值为，求二面角E—AF—C的余弦值.

Answer 1

答案：（1）证明：由四边形ABCD为菱形，∠ABC=60°,可得△ABC为正三角形.

因为E为BC的中点,所以AE⊥BC.

又BC∥AD,因此AE⊥AD.

因为PA⊥平面ABCD,AE平面ABCD,所以PA⊥AE.

而PA平面PAD,AD平面PAD且PA ∩AD=A,

所以AE⊥平面PAD.

又PD平面PAD,所以AE⊥PD.

(2)解:由(1)知AE,AD,AP两两垂直,以A为坐标原点,建立如图所示的空间直角坐标系,又E,F分别为BC,PC的中点,所以A(0,0,0),B(,-1,0),C(,1,0),D(0,2,0),

P(0,0,2),E(,0,0),F(,,1),

所以=(,0,0),=(,,1).

设平面AEF的一法向量为m=(x₁,y₁,z₁),

则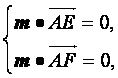

因此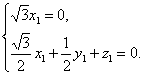

取z₁=-1,则m=(0,2,-1),

因为BD⊥AC,BD⊥PA,PA∩AC=A,

所以BD⊥平面AFC,

故为平面AFC的一法向量.

又=(-,3,0),

所以cos〈m,〉=.

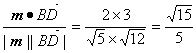因为二面角E—AF—C为锐角,

所以所求二面角的余弦值为.