题目内容
13.设抛物线C1:y2=4x的焦点为F,动点D到点F的距离与到直线x=4的距离之比为$\frac{1}{2}$.(1)求动点D的轨迹C2的方程;
(2)过点F作直线l与曲线C2交于P、Q两点,A1,A2为C2与x轴的交点,直线PA1,QA2相交于点M,直线PA2,QA1相交于点N,求证:MF⊥NF.
分析 (1)利用直接法,即可求动点D的轨迹C2的方程;
(2)(法一)设直线方程,求出M,N的坐标,可得$\overrightarrow{FM}=({3,\frac{{6{y_1}}}{{{x_1}+2}}})$,$\overrightarrow{FN}=({3,\frac{{2{y_1}}}{{{x_1}-2}}})$,利用数量积公式,即可证明结论;(法二)设直线A1P,A2P,A1Q,A2Q的斜率分别为k1,k2,k3,k4,点P坐标为(x1,y1),点Q的坐标为(x2,y2).由(1)可知A1为(-2,0),A2为(2,0).故${k_1}{k_2}=\frac{y_1}{{{x_1}+2}}•\frac{y_1}{{{x_1}-2}}=\frac{y_1^2}{x_1^2-4}=-\frac{3}{4}$,同理可得${k_3}{k_4}=-\frac{3}{4}$,求出M,N的坐标,利用数量积公式,即可证明结论.
解答 解:(1)由y2=4x得F(1,0)…(1分)
设动点D的坐标为(x,y),则$|{DF}|=\sqrt{{{({x-1})}^2}+{y^2}}$
动点D到直线x=4的距离为d=|x-4|
由条件得$\frac{{|{DF}|}}{d}=\frac{1}{2}$,即$\frac{{{{({x-1})}^2}+{y^2}}}{{{{({x-4})}^2}}}=\frac{1}{4}$…(3分)
化简得动点D的轨迹C2的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$…(4分)
(2)(法一)由条件可知l的斜率存在,且不为0.设l的方程为y=k(x-1)
设P(x1,y1),Q(x2,y2)
由$\left\{{\begin{array}{l}{y=k({x-1})}\\{\frac{x^2}{4}+\frac{y^2}{3}=1}\end{array}}\right.$得(3+4k2)x2-8k2x+4k2-12=0
故有${x_1}+{x_2}=\frac{{8{k^2}}}{{3+4{k^2}}},x{\;}_1{x_2}=\frac{{4{k^2}-12}}{{3+4{k^2}}}$…(6分)
由条件可知A1P的方程为:$y=\frac{y_1}{{{x_1}+2}}({x+2})$…①
A2Q的方程为:$y=\frac{y_2}{{{x_2}-2}}({x-2})$…②
①②联立得$x=\frac{{2({\frac{y_2}{{{x_2}-2}}+\frac{y_1}{{{x_1}+2}}})}}{{\frac{y_2}{{{x_2}-2}}-\frac{y_1}{{{x_1}+2}}}}$,即$x=2({1+\frac{2}{{\frac{y_2}{{{x_2}-2}}•\frac{{{x_1}+2}}{y_1}-1}}})$…(8分)
因为$\frac{{{x_1}^2}}{4}+\frac{{{y_1}^2}}{3}=1$,故${y_1}^2=\frac{3}{4}({4-x_1^2})$,所以$\frac{{{x_1}+2}}{y_1}=-\frac{4}{3}\frac{y_1}{{{x_1}-2}}$
因为$\frac{y_2}{{{x_2}-2}}•\frac{{{x_1}+2}}{y_1}=\frac{y_2}{{{x_2}-2}}•({-\frac{4}{3}\frac{y_1}{{{x_1}-2}}})=-\frac{4}{3}•\frac{{{y_1}{y_2}}}{{({{x_1}-2})({{x_2}-2})}}=-\frac{4}{3}•\frac{{{k^2}({{x_1}{x_2}-({{x_1}+{x_2}})+1})}}{{{x_1}x-2({{x_1}+{x_2}})+4}}$=$\frac{{{k^2}({4{k^2}-12-8{k^2}+3+4{k^2}})}}{{4{k^2}-12-2•8{k^2}+12+16{k^2}}}=\frac{{-9{k^2}}}{{4{k^2}}}=-\frac{9}{4}$…(10分)
故$x=2({1+\frac{2}{{({-\frac{4}{3}})•({-\frac{9}{4}})-1}}})=2({1+\frac{2}{2}})=4$…(11分)
把x=4代入$y=\frac{y_1}{{{x_1}+2}}({x+2})$得$y=\frac{{6{y_1}}}{{{x_1}+2}}$,故$M({4,\frac{{6{y_1}}}{{{x_1}+2}}})$…(12分)
同理可得$N({4,\frac{{2{y_1}}}{{{x_1}-2}}})$…(13分)
因为$\overrightarrow{FM}=({3,\frac{{6{y_1}}}{{{x_1}+2}}})$,$\overrightarrow{FN}=({3,\frac{{2{y_1}}}{{{x_1}-2}}})$
故有$\overrightarrow{FM}•\overrightarrow{FN}=9+\frac{{12{y_1}^2}}{x_1^2-4}=9+\frac{{12•\frac{3}{4}•({4-{x^2}})}}{{{x^2}-4}}=9-9=0$
所以MF⊥NF.…(14分)
(法二)设直线A1P,A2P,A1Q,A2Q的斜率分别为k1,k2,k3,k4,点P坐标为(x1,y1),点Q的坐标为(x2,y2).
由(1)可知A1为(-2,0),A2为(2,0).
故${k_1}{k_2}=\frac{y_1}{{{x_1}+2}}•\frac{y_1}{{{x_1}-2}}=\frac{y_1^2}{x_1^2-4}=-\frac{3}{4}$,同理可得${k_3}{k_4}=-\frac{3}{4}$…(6分)
设直线A1P方程为y=k1(x+2)…①
直线A2Q的方程为y=k4(x-2)…②
由①②联立可得$M({\frac{{2({{k_1}+{k_4}})}}{{{k_4}-{k_1}}},\frac{{4{k_1}{k_4}}}{{{k_4}-{k_1}}}})$
同理可得$N({\frac{{2({{k_2}+{k_3}})}}{{{k_2}-{k_3}}},\frac{{4{k_2}{k_3}}}{{{k_2}-{k_3}}}})$
故$\overrightarrow{FM}=({\frac{{3{k_1}+{k_4}}}{{{k_4}-{k_1}}},\frac{{4{k_1}{k_4}}}{{{k_4}-{k_1}}}})$,$\overrightarrow{FN}=({\frac{{3{k_3}+{k_2}}}{{{k_2}-{k_3}}},\frac{{4{k_2}{k_3}}}{{{k_2}-{k_3}}}})$…(8分)
由$\left\{{\begin{array}{l}{y={k_1}({x+2})}\\{\frac{x^2}{4}+\frac{y^2}{3}=1}\end{array}}\right.$可得$({3+4k_1^2}){x^2}+16k_1^2x+16k_1^2-12=0$
因为A1P与曲线C2交于A1,P两点,故$-2{x_1}=\frac{16k_1^2-12}{3+4k_1^2}$
解得${x_1}=\frac{6-8k_1^2}{3+4k_1^2}$,故${y_1}=\frac{{12{k_1}}}{3+4k_1^2}$,即$P({\frac{6-8k_1^2}{3+4k_1^2},\frac{{12{k_1}}}{3+4k_1^2}})$
同理可得$Q({\frac{6-8k_3^2}{3+4k_3^2},\frac{{12{k_3}}}{3+4k_3^2}})$…(10分)
故$\overrightarrow{FP}=({\frac{3-12k_1^2}{3+4k_1^2},\frac{{12{k_1}}}{3+4k_1^2}})$,$\overrightarrow{FQ}=({\frac{3-12k_3^2}{3+4k_3^2},\frac{{12{k_3}}}{3+4k_3^2}})$…(11分)
因为P,F,Q三点共线,故有$\frac{3-12k_1^2}{3+4k_1^2}•\frac{{12{k_3}}}{3+4k_3^2}-\frac{3-12k_3^2}{3+4k_3^2}•\frac{{12{k_1}}}{3+4k_1^2}=0$
化简得(k3-k1)•(1+4k1k3)=0
因为k1≠k3,所以${k_1}{k_3}=-\frac{1}{4}$.
又因为${k_1}{k_2}=-\frac{3}{4}$,${k_3}{k_4}=-\frac{3}{4}$,所以${k_2}{k_4}=-\frac{9}{4}$…(12分)
故$\overrightarrow{FM}•\overrightarrow{FN}=\frac{{({3{k_1}+{k_4}})({3{k_3}+{k_2}})}}{{({{k_4}-{k_1}})({{k_2}-{k_3}})}}+\frac{{16{k_1}{k_2}{k_3}{k_4}}}{{({{k_4}-{k_1}})({{k_2}-{k_3}})}}$=$\frac{{9{k_1}{k_3}+3{k_1}{k_2}+3{k_3}{k_4}+{k_2}{k_4}+16{k_1}{k_2}{k_3}{k_4}}}{{({{k_4}-{k_1}})({{k_2}-{k_3}})}}$=$\frac{{9•({-\frac{1}{4}})+3•({-\frac{3}{4}})+3•({-\frac{3}{4}})+({-\frac{9}{4}})+16•({-\frac{3}{4}})•({-\frac{3}{4}})}}{{({{k_4}-{k_1}})•({{k_2}-{k_3}})}}$=0…(13分)
所以MF⊥NF.…(14分)
点评 本题考查轨迹方程,考查直线与椭圆的位置关系,考查向量知识的运用,考查学生的计算能力,有难度.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案| A. | {0,4,5,2} | B. | {0,4,5} | C. | {4,5,2} | D. | {4,5} |
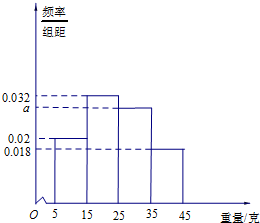 测量马口鱼性成熟时重量,从大量马口鱼中随机抽取100尾作为样本,测出它们的重量(单位:克),重量分组区间为(5,15],(15,25],(25,35],(35,45],由此得到重量样本的频率分布直方图,如图.
测量马口鱼性成熟时重量,从大量马口鱼中随机抽取100尾作为样本,测出它们的重量(单位:克),重量分组区间为(5,15],(15,25],(25,35],(35,45],由此得到重量样本的频率分布直方图,如图.