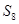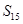题目内容
等差数列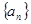 的前
的前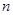 项和为
项和为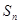 ,若
,若 ,则
,则 ( )
( )
| A.18 | B.36 | C.45 | D.60 |
C
解析试题分析:因为 ,所以
,所以 ,所以
,所以 。
。
考点:等差数列的性质;等差数列的前n项和。
点评:数列掌握等差数列前n项和的性质: 。属于基础题型。
。属于基础题型。

练习册系列答案
相关题目
在等差数列 中,
中,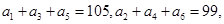 以
以 表示数列
表示数列 的前
的前 项和,则使
项和,则使 达到最大值的
达到最大值的 是( )
是( )
A.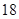 | B.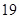 | C.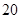 | D.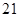 |
已知等差数列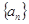 中
中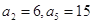 ,若
,若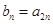 ,则数列
,则数列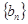 的前
的前 项和等于( )
项和等于( )
A.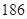 | B. | C.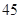 | D.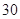 |
已知等差数列 的前
的前 项和为
项和为 ,则数列
,则数列 的前100项和为
的前100项和为
A. | B. | C. | D. |
已知Sn是等差数列{an}(nÎN*)的前n项和,且S6>S7>S5,有下列四个命题,假命题的是( )
| A.公差d<0 | B.在所有Sn<0中,S13最大 |
| C.满足Sn>0的n的个数有11个 | D.a6>a7 |
如果等差数列 中,
中,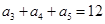 ,那么
,那么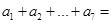 ( )
( )
| A.14 | B.21 | C.28 | D.35 |
已知数列 满足
满足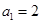 ,
,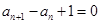
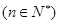 ,则此数列的通项
,则此数列的通项 等于( )
等于( )
A.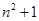 | B.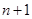 | C.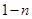 | D.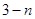 |
若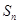 是等差数列
是等差数列 的前n项和,
的前n项和,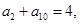 则
则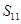 的值为( )
的值为( )
| A.12 | B.22 | C.18 | D.44 |
 的公差为
的公差为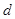 ,前
,前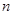 项和为
项和为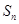 ,当首项
,当首项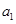 和
和 是一个定值,则下列各数中也为定值的是 ( )
是一个定值,则下列各数中也为定值的是 ( )