题目内容
已知 (a,b为常数)为奇函数,且过点
(a,b为常数)为奇函数,且过点 .
.(1)求f(x)的表达式;
(2)定义正数数列
 ,证明:数列
,证明:数列 是等比数列;
是等比数列;(3)令
 的前n项和,求使
的前n项和,求使 成立的最小n值.
成立的最小n值.
【答案】分析:(1)根据函数为奇函数和过点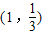 ,求出a,b,确定出f(x)的解析式.
,求出a,b,确定出f(x)的解析式.
(2)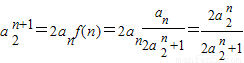 ,化简可得数列{
,化简可得数列{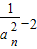 }是以2为首项,
}是以2为首项, 为公比的等比数列.
为公比的等比数列.
(3)bn为等比数列,根据等比数列的求和公式求出Sn,解出不等式中n的范围,从而确定n的最小值.
解答:解:(1)∵f(x)=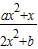 为奇函数,∴f(-x)=
为奇函数,∴f(-x)=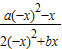 =
=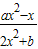 =-
=-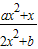 =-f(x),
=-f(x),
∴a=0;
又f(x)过点(1, ),∴f(1)=
),∴f(1)=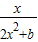 =
=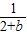 =
= ,∴b=1.∴f(x)=
,∴b=1.∴f(x)=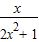
(2)∵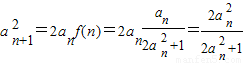
∴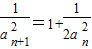 ,,
,,
∴ ∴数列{
∴数列{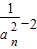 }是以2为首项,
}是以2为首项, 为公比的等比数列.
为公比的等比数列.
(3)∵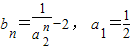
∴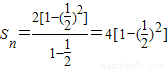
又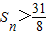 ,即
,即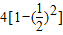
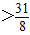
∴n>5
∴满足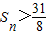 的最小为6.
的最小为6.
点评:本题是数列与函数的综合题,考查了等比数列的证明,等比数列的求和,以及不等式的解法,综合性比较强,应该灵活掌握.
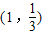 ,求出a,b,确定出f(x)的解析式.
,求出a,b,确定出f(x)的解析式.(2)
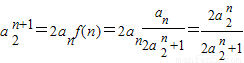 ,化简可得数列{
,化简可得数列{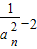 }是以2为首项,
}是以2为首项, 为公比的等比数列.
为公比的等比数列.(3)bn为等比数列,根据等比数列的求和公式求出Sn,解出不等式中n的范围,从而确定n的最小值.
解答:解:(1)∵f(x)=
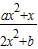 为奇函数,∴f(-x)=
为奇函数,∴f(-x)=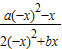 =
=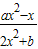 =-
=-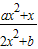 =-f(x),
=-f(x),∴a=0;
又f(x)过点(1,
 ),∴f(1)=
),∴f(1)=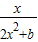 =
=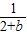 =
= ,∴b=1.∴f(x)=
,∴b=1.∴f(x)=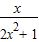
(2)∵
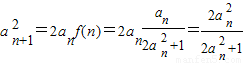
∴
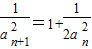 ,,
,,∴
 ∴数列{
∴数列{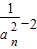 }是以2为首项,
}是以2为首项, 为公比的等比数列.
为公比的等比数列.(3)∵
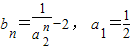
∴
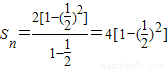
又
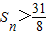 ,即
,即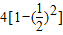
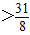
∴n>5
∴满足
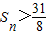 的最小为6.
的最小为6.点评:本题是数列与函数的综合题,考查了等比数列的证明,等比数列的求和,以及不等式的解法,综合性比较强,应该灵活掌握.

练习册系列答案
相关题目
 (a,b为常数,a¹
0)满足f(2)=1,且
(a,b为常数,a¹
0)满足f(2)=1,且 有唯一解.(1)求f(x)的表达式;(2)若记
有唯一解.(1)求f(x)的表达式;(2)若记 ,且
,且 ,求
,求 .
. (a,b为常数),在R上连续,则a的值是
(a,b为常数),在R上连续,则a的值是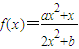 (a,b为常数)为奇函数,且过点
(a,b为常数)为奇函数,且过点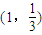 .
. ,证明:数列
,证明:数列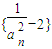 是等比数列;
是等比数列;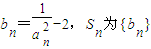 的前n项和,求使
的前n项和,求使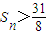 成立的最小n值.
成立的最小n值.