Question

【题目】已知椭圆的焦点在x轴上，短轴长为4，离心率为 ．
（1）求椭圆的标准方程；
（2）若直线l过该椭圆的左焦点，交椭圆于M、N两点，且 ，求直线l的方程．

Answer 1

【答案】
（1）解： ，椭圆的标准方程：
（2）解：由题意知，直线l的斜率存在，所以设直线方程为：y=k（x+1），

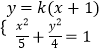，联立得：（5k2+4）x2+10k2x+5k2﹣20=0，

∴ ，

则：

= = ，

∵ ，

∴

即：

即： ，

所以，k=±1，所以直线方程为：y=x+1或y=﹣x﹣1

【解析】（1）由短轴长可得b值，由离心率为 可得 = ，结合a2=b2+c2即可求得a值，即可得出椭圆的方程；（2）设直线方程为：y=k（x+1），联立方程组消掉y得到x的二次方程，设M（x1 ， y1），N（x2 ， y2），由韦达定理及弦长公式即可表示弦长|MN|，最后利用弦长建立等式，即可求出直线l的方程．
【考点精析】认真审题，首先需要了解一般式方程(直线的一般式方程：关于的二元一次方程（A，B不同时为0）)，还要掌握椭圆的标准方程(椭圆标准方程焦点在x轴：，焦点在y轴：)的相关知识才是答题的关键．