题目内容
20.已知函数f(x)=excosx-x.(1)求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)求函数f(x)在区间[0,$\frac{π}{2}$]上的最大值和最小值.
分析 (1)求出f(x)的导数,可得切线的斜率和切点,由点斜式方程即可得到所求方程;
(2)求出f(x)的导数,再令g(x)=f′(x),求出g(x)的导数,可得g(x)在区间[0,$\frac{π}{2}$]的单调性,即可得到f(x)的单调性,进而得到f(x)的最值.
解答 解:(1)函数f(x)=excosx-x的导数为f′(x)=ex(cosx-sinx)-1,
可得曲线y=f(x)在点(0,f(0))处的切线斜率为k=e0(cos0-sin0)-1=0,
切点为(0,e0cos0-0),即为(0,1),
曲线y=f(x)在点(0,f(0))处的切线方程为y=1;
(2)函数f(x)=excosx-x的导数为f′(x)=ex(cosx-sinx)-1,
令g(x)=ex(cosx-sinx)-1,
则g(x)的导数为g′(x)=ex(cosx-sinx-sinx-cosx)=-2ex•sinx,
当x∈[0,$\frac{π}{2}$],可得g′(x)=-2ex•sinx≤0,
即有g(x)在[0,$\frac{π}{2}$]递减,可得g(x)≤g(0)=0,
则f(x)在[0,$\frac{π}{2}$]递减,
即有函数f(x)在区间[0,$\frac{π}{2}$]上的最大值为f(0)=e0cos0-0=1;
最小值为f($\frac{π}{2}$)=e${\;}^{\frac{π}{2}}$cos$\frac{π}{2}$-$\frac{π}{2}$=-$\frac{π}{2}$.
点评 本题考查导数的运用:求切线的方程和单调区间、最值,考查化简整理的运算能力,正确求导和运用二次求导是解题的关键,属于中档题.

练习册系列答案
相关题目
10.某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
以最高气温位于各区间的频率代替最高气温位于该区间的概率.
(1)求六月份这种酸奶一天的需求量X(单位:瓶)的分布列;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量n(单位:瓶)为多少时,Y的数学期望达到最大值?
| 最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
| 天数 | 2 | 16 | 36 | 25 | 7 | 4 |
(1)求六月份这种酸奶一天的需求量X(单位:瓶)的分布列;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量n(单位:瓶)为多少时,Y的数学期望达到最大值?
8.某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
以最高气温位于各区间的频率估计最高气温位于该区间的概率.
(1)求六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.
| 最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
| 天数 | 2 | 16 | 36 | 25 | 7 | 4 |
(1)求六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.
5.若双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线被圆(x-2)2+y2=4所截得的弦长为2,则C的离心率为( )
| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
14.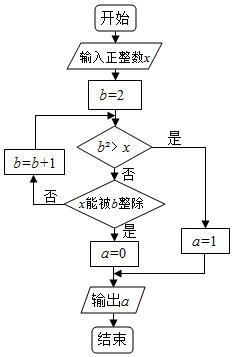 执行两次如图所示的程序框图,若第一次输入的x值为7,第二次输入的x值为9,则第一次,第二次输出的a值分别为( )
执行两次如图所示的程序框图,若第一次输入的x值为7,第二次输入的x值为9,则第一次,第二次输出的a值分别为( )
 执行两次如图所示的程序框图,若第一次输入的x值为7,第二次输入的x值为9,则第一次,第二次输出的a值分别为( )
执行两次如图所示的程序框图,若第一次输入的x值为7,第二次输入的x值为9,则第一次,第二次输出的a值分别为( )| A. | 0,0 | B. | 1,1 | C. | 0,1 | D. | 1,0 |