题目内容
22、在直径是AB的半圆上有两点M，N，设AN与BM的交点是P．求证：AP•AN+BP•BM=AB2．分析：作PE⊥AB于E，先证明P，E，B，N四点共圆，P，E，A，M四点共圆，得到两对乘积式，后相加即可得到结论．
解答：
证明：作PE⊥AB于E∵AB为直径，
∴∠ANB=∠AMB=90°
∴P，E，B，N四点共圆，P，E，A，M四点共圆．
AE•AB=AP•AN（1）
BE•AB=BP•BM（2）
（1）+（2）得AB（AE+BE）=AP•AN+BP•BM
即AP•AN+BP•BM=AB2
证明：作PE⊥AB于E∵AB为直径，∴∠ANB=∠AMB=90°
∴P，E，B，N四点共圆，P，E，A，M四点共圆．
AE•AB=AP•AN（1）
BE•AB=BP•BM（2）
（1）+（2）得AB（AE+BE）=AP•AN+BP•BM
即AP•AN+BP•BM=AB2
点评：本题主要考查了与圆有关的比例线段，特别是证明四点共圆的方法，属于基础题．
练习册系列答案
相关题目
.
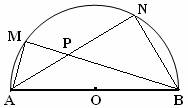如图，在直径是AB的半圆上有两个不同的点M、N,设AN与BM的交点是P.求证：
.
