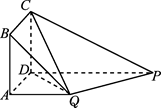
题目内容
四面体ABCD中，已知AB=CD=
，AC=BD=
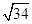，AD=BC=
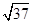，则四面体ABCD的外接球的表面积为（ ）
| A．25p | B．45p | C．50p | D．100p |
C
解析试题分析：由题意可采用割补法，考虑到四面体
的四个面为全等的三角形，所以可在其每个面补上一个以
为三边的三角形作为底面，且以分别
长、两两垂直的侧棱的三棱锥，从而可得到一个长、宽、高分别为的长方体，并且
，则有
（
为球的半径），得
，所以球的表面积为
，故正确答案为C.
考点：空间组合体间联系、球的表面积.
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
一个几何体的三视图如图所示，则该几何体的体积为（ ）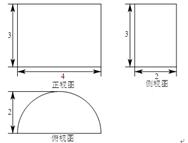
A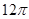． | B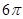． | C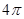． | D． |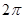
一个空间几何体的三视图如图，则该几何体的体积为（ ）
A． | B． | C． | D． |
已知某个几何体的三视图如下，根据图中标出的尺寸（单位：cm），可得这个几何体的体积是
A． | B． | C． | D． |
若两个球的表面积之比为1：4，则这两个球的体积之比为（ ）
| A．1：2, | B．1：4, | C．1：8, | D．1：16 |
某空间几何体的三视图如图所示，则该几何体的体积为（ ）
A． | B． | C． | D． |