Question

已知圆O：x²+y²=4，动点P（t，0）（-2≤t≤2），曲线C：y=3|x-t|．曲线C与圆O相交于两个不同的点M，N
（1）若t=1，求线段MN的中点P的坐标；
（2）求证：线段MN的长度为定值；
（3）若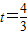，m，n，s，p均为正整数．试问：曲线C上是否存在两点A（m，n），B（s，p）（11），使得圆O上任意一点到点A的距离与到点B的距离之比为定值k（k＞1）？若存在请求出所有的点A，B；若不存在请说明理由．

Answer 1

【答案】分析：（1）将曲线C的方程代入圆的方程，消去y得到关于x的一元二次方程，再结合根系数的关系利用中点坐标公式即可求得P的坐标；
（2）利用将曲线C的方程代入圆的方程，消去y得到的方程，结合根与系数的关系，利用两点间的距离公式即可求出线段MN的长度为定值；
（3）对于存在性问题，可先假设存在，即假设存在两点A（m，n），B（s，p）（11），使得圆O上任意一点到点A的距离与到点B的距离之比为定值，再建立等式求出A，B的坐标，若出现矛盾，则说明假设不成立，即不存在；否则存在．
解答：解：（1）设M（x₁，y₁），N（x₂，y₂）（x₁＜1＜x₂），P（x，y）
由，
所以=
所以---------------------------（6分）
（2），
，
，
=，
，为定值．---------------------------------（4分）
（3）设，

消去m，n得
所以s=p=1，，此时m=n=2，又A（2，2），B（1，1）在曲线C上
所以仅有A（2，2），B（1，1）符合．----------------------------------------（6分）
点评：本小题主要考查中点坐标公式、两点间的距离公式极值、导数、直线与圆的位置关系等基本知识，考查方程思想、化归以及数形结合等数学思想方法，考查分析问题、解决问题的能力．