题目内容
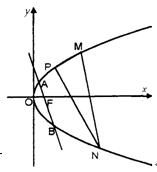
过抛物线L: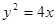 的焦点F的直线l交此抛物线于A、B两点,
的焦点F的直线l交此抛物线于A、B两点,
①求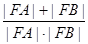 ;
;
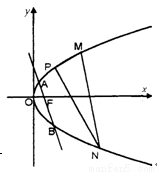
②记坐标原点为O,求△OAB的重心G的轨迹方程.
③点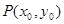 为抛物线L上一定点,M、N为抛物线上两个动点,且满足
为抛物线L上一定点,M、N为抛物线上两个动点,且满足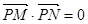 ,当点M、N在抛物线上运动时,证明直线MN过定点。
,当点M、N在抛物线上运动时,证明直线MN过定点。
【答案】
①
②
③证明见解析。
【解析】①由F(1,0),设直线l的方程为
 联立得
联立得
 ……2分
……2分
由
 …………4分
…………4分
②设 …………5分
…………5分
由 ……7分
……7分
化简得轨迹方程为  …………9分
…………9分
③证明:由直线MN的方程不可能与x轴平行
可设直线MN的方程为
 分别相减得
分别相减得 
由
 ,
,
∴
即
 (*式)
…………11分
(*式)
…………11分
联立 
有 ,
,
所以
 ,代入直线MN的方程有
,代入直线MN的方程有 

练习册系列答案
相关题目
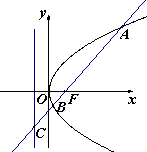 如图,过抛物线y2=3x的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,则|AF|=( )
如图,过抛物线y2=3x的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,则|AF|=( )