Question

已知函数f（x）=e^x-1-x．
（Ⅰ）求y=f（x）在点（1，f（1））处的切线方程；
（Ⅱ）若存在x₀∈[-1，ln

4

3

]，满足a-e^x+1+x＜0成立，求a的取值范围；
（Ⅲ）当x≥0时，f（x）≥（t-1）x恒成立，求t的范围．

Answer 1

分析：（Ⅰ）利用导数的几何意义求切线方程；
（Ⅱ）由a-e^x+1+x＜0得a＜e^x-1-x，然后求出函数e^x-1-x的最大值；
（Ⅲ）将不等式f（x）≥（t-1）x化简为e^x-1≥tx，利用图象关系求t的取值范围．

解答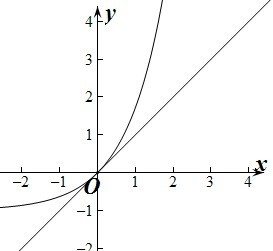：解：（Ⅰ）因为f（1）=e-2，函数的导数为f'（x）=e^x-1，所以f'（1）=e-1，
所以函数在（1，e-2）处的切线方程为：y-（e-1）=（e-1）（x-1），即y=（e-1）x．
（Ⅱ）要使a-e^x+1+x＜0成立，即a＜e^x-1-x，只有求出函数e^x-1-x在[-1，ln

4

3

]的最大值，即可．
设f（x）=e^x-1-x，函数的导数为f'（x）=e^x-1，由f'（x）=e^x-1=0，
解得x=0，当x＞0，f'（x）＞0，此时函数递增．当x＜0，f'（x）＜0，此时函数递减．
所以当x=0时，函数f（x）=e^x-1-x取的极小值f（0）=0，同时也是最小值．
f（-1）=

1

e

-1+1=

1

e

，f（ln

4

3

）=eln

4

3

-ln

4

3

-1=

4

3

-1-ln

4

3

=

1

3

-ln

4

3

，
因为f（-1）＞f(ln

4

3

)，所以在[-1，ln

4

3

]上函数的最大值为f（-1）=

1

e

．
所以要使a＜e^x-1-x，成立，所以有a＜

1

e

．
即a的取值范围是a＜

1

e

．
（Ⅲ）当x≥0时，f（x）≥（t-1）x，所以e^x-1≥tx，
设g（x）=e^x-1，则g'（x）=e^x，当x≥0时，g'（x）=e^x≥1，
如图：要使e^x-1≥tx成立，则有t≤1，所以t的范围t≤1．

点评：本题的考点是导数的几何意义以及利用导数求函数的最值，其中第三问需要利用数形结合思想去解决．