题目内容
在△ABC中，角A，B，C的对边分别是a，b，c。设向量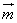
=（a，cosB），
=(b，cosA)， 且
//
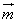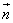且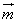
≠
。
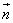(1)求证：A+B=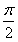
，并求出sinA+sinB的取值范围；
(2)设sinA+sinB=t，将y=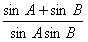
表示成t的函数f(t)，并求出y=f(t)的值域。
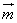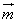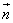=（a，cosB），=(b，cosA)， 且//且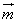≠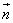。(1)求证：A+B=
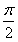，并求出sinA+sinB的取值范围； (2)设sinA+sinB=t，将y=
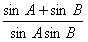表示成t的函数f(t)，并求出y=f(t)的值域。 解：（1）
acosA-bcosB=0
sinAcosA-sinBcosB=0sin2A=sin2B，
从而2A+2B=π或2A=2B（舍去，∵
），
∴A+B=
，
∴sinA+sinB=sinA+cosA=
，
∴sinA+sinB
（2）
在t
上为减函数，
∴
，
acosA-bcosB=0sinAcosA-sinBcosB=0sin2A=sin2B，从而2A+2B=π或2A=2B（舍去，∵
），∴A+B=
，∴sinA+sinB=sinA+cosA=
，∴sinA+sinB
（2）
在t上为减函数，∴
，
练习册系列答案
通城学典默写能手系列答案
相关题目
在△ABC中，角A、B、C所对的边分别为a，b，c，若b2+c2-a2=
bc，且b=
a，则下列关系一定不成立的是（ ）
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |