题目内容
如图,有一正方形钢板ABCD缺损一角(图中的阴影部分),边缘线OC是以直线AD为对称轴,以线段AD的中点O为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.若正方形的边长为2米,问如何画切割线EF,可使剩余的直角梯形的面积最大?并求其最大值.
【答案】分析:根据题意建立坐标系,有题意可得抛物线的方程为 ,设出切点得出切线方程求出点E、F的坐标,进而表示出梯形的面积再结合二次函数的性质求出面积最大值,最终解决实际问题.
,设出切点得出切线方程求出点E、F的坐标,进而表示出梯形的面积再结合二次函数的性质求出面积最大值,最终解决实际问题.
解答: 解:以O为原点,直线AD为y轴,建立如图所示的直角坐标系,依题意可设抛物线弧OC的方程为y=ax2(0≤x≤2)
解:以O为原点,直线AD为y轴,建立如图所示的直角坐标系,依题意可设抛物线弧OC的方程为y=ax2(0≤x≤2)
∵点C的坐标为(2,1),
∴22a=1,
故边缘线OC的方程为 .
.
要使梯形ABEF的面积最大,则EF所在的直线必与抛物线弧OC相切,设切点坐标为 ,
,
∵ ,
,
∴直线EF的方程可表示为 ,即
,即 ,
,
由此可求得 ,
, .
.
∴ ,
, ,
,
设梯形ABEF的面积为S(t),则 =
= =
= =
= .
.
∴当t=1时, .,
.,
故S(t)的最大值为2.5.此时|AF|=0.75,|BE|=1.75.
答:当AF=0.75m,BE=1.75m时,可使剩余的直角梯形的面积最大,其最大值为2.5m2.
点评:解应用题常用的方法是依据题意建立等量关系,构造数学模型利用函数的性质进行求解,而有些应用题有明显的几何意义,可以考虑利用解析法根据题意建立适当的坐标系,构造曲线方程,利用曲线的性质进行求解.
 ,设出切点得出切线方程求出点E、F的坐标,进而表示出梯形的面积再结合二次函数的性质求出面积最大值,最终解决实际问题.
,设出切点得出切线方程求出点E、F的坐标,进而表示出梯形的面积再结合二次函数的性质求出面积最大值,最终解决实际问题.解答:
 解:以O为原点,直线AD为y轴,建立如图所示的直角坐标系,依题意可设抛物线弧OC的方程为y=ax2(0≤x≤2)
解:以O为原点,直线AD为y轴,建立如图所示的直角坐标系,依题意可设抛物线弧OC的方程为y=ax2(0≤x≤2)∵点C的坐标为(2,1),
∴22a=1,

故边缘线OC的方程为
 .
.要使梯形ABEF的面积最大,则EF所在的直线必与抛物线弧OC相切,设切点坐标为
 ,
,∵
 ,
,∴直线EF的方程可表示为
 ,即
,即 ,
,由此可求得
 ,
, .
.∴
 ,
, ,
,设梯形ABEF的面积为S(t),则
 =
= =
= =
= .
.∴当t=1时,
 .,
.,故S(t)的最大值为2.5.此时|AF|=0.75,|BE|=1.75.
答:当AF=0.75m,BE=1.75m时,可使剩余的直角梯形的面积最大,其最大值为2.5m2.
点评:解应用题常用的方法是依据题意建立等量关系,构造数学模型利用函数的性质进行求解,而有些应用题有明显的几何意义,可以考虑利用解析法根据题意建立适当的坐标系,构造曲线方程,利用曲线的性质进行求解.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 如图,有一正方形钢板ABCD缺损一角(图中的阴影部分),边缘线OC是以直线AD为对称轴,以线段AD的中点O为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.若正方形的边长为2米,问如何画切割线EF,可使剩余的直角梯形的面积最大?并求其最大值.
如图,有一正方形钢板ABCD缺损一角(图中的阴影部分),边缘线OC是以直线AD为对称轴,以线段AD的中点O为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.若正方形的边长为2米,问如何画切割线EF,可使剩余的直角梯形的面积最大?并求其最大值.
 缺损一角(图中的阴影部分),边缘线
缺损一角(图中的阴影部分),边缘线 是以直线AD为对称轴,以线段
是以直线AD为对称轴,以线段 的中点
的中点 为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.若正方形的边长为2米,问如何画切割线
为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.若正方形的边长为2米,问如何画切割线 ,可使剩余的直角梯形的面积最大?并求其最大值.
,可使剩余的直角梯形的面积最大?并求其最大值.
 缺损一角(图中的阴影部分),边缘线
缺损一角(图中的阴影部分),边缘线 是以直线AD为对称轴,以线段
是以直线AD为对称轴,以线段 的中点
的中点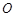 为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.若正方形的边长为2米,问如何画切割线
为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.若正方形的边长为2米,问如何画切割线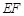 ,可使剩余的直角梯形的面积最大?并求其最大值.
,可使剩余的直角梯形的面积最大?并求其最大值.