题目内容
已知椭圆 的左、右顶点分别为A、B,曲线E是以椭圆中心为顶点,B为焦点的抛物线.
的左、右顶点分别为A、B,曲线E是以椭圆中心为顶点,B为焦点的抛物线.
(Ⅰ)求曲线E的方程;
(Ⅱ)直线 与曲线E交于不同的两点M、N,当
与曲线E交于不同的两点M、N,当 时,求直线l的倾斜角θ的取值范围.
时,求直线l的倾斜角θ的取值范围.
解:(Ⅰ)依题意得:A(-2,0),B(2,0),
∴曲线E的方程为y2=8x.…(4分)
(Ⅱ)由 得:kx2-(2k+8)x+k=0,
得:kx2-(2k+8)x+k=0,
由 ?k>0…(7分)
?k>0…(7分)
设M(x1,y1),N(x2,y2),则: ,
,
∴ …(9分)
…(9分)
=
∴0<k≤1,∴ .…(12分)
.…(12分)
分析:(Ⅰ)依题意可求A,B进而可求抛物线E的方程
(Ⅱ)由 得:kx2-(2k+8)x+k=0,由
得:kx2-(2k+8)x+k=0,由 可求k的范围,再由
可求k的范围,再由 可求k的范围,进而可求θ的范围
可求k的范围,进而可求θ的范围
点评:本题主要考查了利用抛物线的性质求解抛物线的方程,直线与抛物线方程的相交的处理中,要注意方程的根与系数的关系的应用.
∴曲线E的方程为y2=8x.…(4分)
(Ⅱ)由
 得:kx2-(2k+8)x+k=0,
得:kx2-(2k+8)x+k=0,由
 ?k>0…(7分)
?k>0…(7分)设M(x1,y1),N(x2,y2),则:
 ,
,∴
 …(9分)
…(9分)=

∴0<k≤1,∴
 .…(12分)
.…(12分)分析:(Ⅰ)依题意可求A,B进而可求抛物线E的方程
(Ⅱ)由
 得:kx2-(2k+8)x+k=0,由
得:kx2-(2k+8)x+k=0,由 可求k的范围,再由
可求k的范围,再由 可求k的范围,进而可求θ的范围
可求k的范围,进而可求θ的范围点评:本题主要考查了利用抛物线的性质求解抛物线的方程,直线与抛物线方程的相交的处理中,要注意方程的根与系数的关系的应用.

练习册系列答案
相关题目
 在平面直角坐标系
在平面直角坐标系 在平面直角坐标系
在平面直角坐标系 的左、右顶点分别为M、N,P为椭圆上任意一点,且直线PM的斜率的取值范围是[
的左、右顶点分别为M、N,P为椭圆上任意一点,且直线PM的斜率的取值范围是[ ,2],则直线PN的斜率的取值范围是( )
,2],则直线PN的斜率的取值范围是( ) B.
B. C.[-8,-2] D.[2,8]
C.[-8,-2] D.[2,8] 在平面直角坐标系
在平面直角坐标系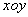 中,如图,已知椭圆
中,如图,已知椭圆 的左、右顶点为A、B,右焦点为F。设过点T(
的左、右顶点为A、B,右焦点为F。设过点T( )的直线TA、TB与椭圆分别交于点M
)的直线TA、TB与椭圆分别交于点M 、
、 ,其中m>0,
,其中m>0, 。
。 ,求点P的轨迹;
,求点P的轨迹; ,求点T的坐标;
,求点T的坐标; ,求证:直线MN必过x轴上的一定点(其坐标与m无关)。
,求证:直线MN必过x轴上的一定点(其坐标与m无关)。 本小题满分12分)
本小题满分12分) 的左、右顶点分别为
的左、右顶点分别为 曲线
曲线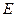 是以椭圆中心为顶点,
是以椭圆中心为顶点, 为焦点的抛物线.
为焦点的抛物线.
 与曲线
与曲线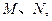 当
当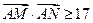 时,求直线
时,求直线 的倾斜角
的倾斜角 的取值范围.
的取值范围.