题目内容
（几何证明选讲选做题）如图，EF是梯形ABCD的中位线，记梯形ABFE的面积为S1，梯形CDEF的面积为S2，若| AB |
| CD |
| 1 |
| 2 |
| AB |
| EF |
| 2 |
| 3 |
| 2 |
| 3 |
| S1 |
| S2 |
| 5 |
| 7 |
| 5 |
| 7 |
分析：①求
利用梯形的中位线定理即可得出；②利用梯形的面积公式和梯形中位线的性质即可得出．
| AB |
| CD |
解答：解：①设AB=x，∵
=
，∴CD=2x，
∵EF是梯形ABCD的中位线，∴EF=
(AB+CD)=
，∴
=
=
．
②设h1是梯形ABFE的高，h2为梯形CDEF的高，则h1=h2．
∴
=
=
=
．
故答案为
，
．
| AB |
| CD |
| 1 |
| 2 |
∵EF是梯形ABCD的中位线，∴EF=
| 1 |
| 2 |
| 3x |
| 2 |
| AB |
| EF |
| x | ||
|
| 2 |
| 3 |
②设h1是梯形ABFE的高，h2为梯形CDEF的高，则h1=h2．
∴
| S1 |
| S2 |
| ||
|
x+
| ||
|
| 5 |
| 7 |
故答案为
| 2 |
| 3 |
| 5 |
| 7 |
点评：熟练掌握梯形的面积公式和梯形中位线的性质是解题的关键．
练习册系列答案
相关题目
（几何证明选讲选做题）
（几何证明选讲选做题）如图，四边形ABCD内接于⊙O，AB为⊙O的直径，直线MN切⊙O于D，∠MDA=60°，则∠BCD=
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）
（几何证明选讲选做题）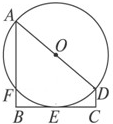
（几何证明选讲选做题）