题目内容
已知椭圆中心在坐标原点O,焦点在坐标轴上,直线y=x+1与该椭圆相交于P和Q点,且OP⊥OQ,|PQ|=
解析:设直线y=x+1与椭圆mx2+ny2=1(m>0,n>0)的交点为P(x1,y1)、Q(x2,y2),联立方程组 消去y,得(m+n)x2+2nx+(n-1)=0.
消去y,得(m+n)x2+2nx+(n-1)=0.
∴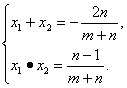 又OP⊥OQ,∴x1x2+y1y2=0,即2x1x2+(x1+x2)+1=0.从而得出
又OP⊥OQ,∴x1x2+y1y2=0,即2x1x2+(x1+x2)+1=0.从而得出
2·![]()
![]() +1=0,解得m+n=2. ①
+1=0,解得m+n=2. ①
由|PQ|=![]() ,得
,得![]()
![]() =
=![]() ,
,
即![]()
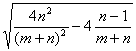 =
=![]() ,解得mn=
,解得mn=![]() . ②
. ②
联立①②解得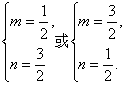 故所求椭圆方程为
故所求椭圆方程为![]() 或
或![]() .
.

练习册系列答案
相关题目