题目内容
下列命题中,真命题是( )A.存在
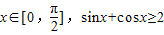
B.任意
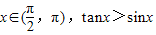
C.存在x∈R,x2+x=-1
D.任意x∈(3,+∞),x2>2x+1
【答案】分析:根据正弦型函数的图象和性质,可得当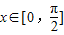 时,sinx+cosx的取值范围,进而判断A的真假;
时,sinx+cosx的取值范围,进而判断A的真假;
根据三角函数在各象限的符号,分析出在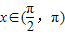 时,tanx与sinx的大小,进而判断B的真假;
时,tanx与sinx的大小,进而判断B的真假;
根据方程根的个数与△的关系,判断方程x2+x=-1根的存在性,进而判断C的真假;
根据二次函数的图象和性质,分析不等式x2+x=-1是否恒成立,可判断D的真假.
解答:解:当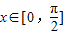 时,sinx+cosx∈[1,
时,sinx+cosx∈[1,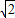 ],而2∉[1,
],而2∉[1,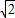 ],故A错误;
],故A错误;
当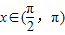 时,tanx<0,sinx>0,故tanx<sinx恒成立,故B错误;
时,tanx<0,sinx>0,故tanx<sinx恒成立,故B错误;
方程x2+x+1=0的△=1-4=-3<0,故方程无实根,故C错误;
任意x∈(3,+∞),x2-2x-1=(x-1)2-2>2>0恒成立,即x2>2x+1恒成立,故D正确
故选D
点评:本题以命题的真假判断为载体,考查了三角函数的图象和性质,方程根的个数判断及二次不等式恒成立问题,是方程、函数、不等式的简单综合应用.
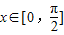 时,sinx+cosx的取值范围,进而判断A的真假;
时,sinx+cosx的取值范围,进而判断A的真假;根据三角函数在各象限的符号,分析出在
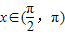 时,tanx与sinx的大小,进而判断B的真假;
时,tanx与sinx的大小,进而判断B的真假;根据方程根的个数与△的关系,判断方程x2+x=-1根的存在性,进而判断C的真假;
根据二次函数的图象和性质,分析不等式x2+x=-1是否恒成立,可判断D的真假.
解答:解:当
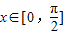 时,sinx+cosx∈[1,
时,sinx+cosx∈[1,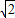 ],而2∉[1,
],而2∉[1,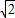 ],故A错误;
],故A错误;当
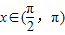 时,tanx<0,sinx>0,故tanx<sinx恒成立,故B错误;
时,tanx<0,sinx>0,故tanx<sinx恒成立,故B错误;方程x2+x+1=0的△=1-4=-3<0,故方程无实根,故C错误;
任意x∈(3,+∞),x2-2x-1=(x-1)2-2>2>0恒成立,即x2>2x+1恒成立,故D正确
故选D
点评:本题以命题的真假判断为载体,考查了三角函数的图象和性质,方程根的个数判断及二次不等式恒成立问题,是方程、函数、不等式的简单综合应用.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
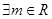 ,使函数
,使函数 是偶函数
是偶函数 ,使函数
,使函数 ≤0
≤0 =-1
=-1