题目内容
已知函数f(x)=2x
(1)设函数y=f(x)的反函数为y=g(x),求函数y=g(x2-2x-3)的单调递增区间;
(2)求满足不等式f(|x+1|-|x-1|) 的x的取值范围.
的x的取值范围.
解:(1)由f(x)=2x,得y=g(x)=log2x,则y=g(x2-2x-3)=log2(x2-2x-3),
由x2-2x-3>0,得x<-1或x>3,
所以函数y=g(x2-2x-3)的定义域为(-∞,-1)∪(3,+∞),
因为y=log2u单调递增,u=x2-2x-3在(3+∞)上递增,
所以y=log2(x2-2x-3)的递增区间为(3+∞);
(2)f(|x+1|-|x-1|) ,即
,即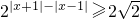 ,
,
所以|x+1|-|x-1| ,
,
①当x≤-1时,不等式可化为-(x+1)-(1-x)≥ ,即-2≥
,即-2≥ ,无解;
,无解;
②当-1<x≤1时,不等式可化为(x+1)-(1-x) ,即2x
,即2x ,解得x
,解得x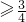 ,
,
所以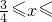 1;
1;
③当x>1时,不等式可化为(x+1)-(x-1) ,即2
,即2 ,
,
所以x>1;
综上,x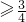 ,即不等式f(|x+1|-|x-1|)
,即不等式f(|x+1|-|x-1|) 的x的取值范围为x
的x的取值范围为x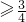 .
.
分析:(1)先由f(x)求得g(x),进而得到y=g(x2-2x-3),根据复合函数单调性的判断方法可求得函数的单调增区间,注意函数的定义域;
(2)表示出不等式,利用指数函数的单调性可得|x+1|-|x-1| ,按照x≤-1,-1<x≤1,x>1三种情况讨论去掉绝对值符号即可解得不等式;
,按照x≤-1,-1<x≤1,x>1三种情况讨论去掉绝对值符号即可解得不等式;
点评:本题考查复合函数的单调性、反函数以及绝对值不等式的求解,考查分类讨论思想,综合性较强,难度较大.
由x2-2x-3>0,得x<-1或x>3,
所以函数y=g(x2-2x-3)的定义域为(-∞,-1)∪(3,+∞),
因为y=log2u单调递增,u=x2-2x-3在(3+∞)上递增,
所以y=log2(x2-2x-3)的递增区间为(3+∞);
(2)f(|x+1|-|x-1|)
 ,即
,即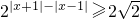 ,
,所以|x+1|-|x-1|
 ,
,①当x≤-1时,不等式可化为-(x+1)-(1-x)≥
 ,即-2≥
,即-2≥ ,无解;
,无解;②当-1<x≤1时,不等式可化为(x+1)-(1-x)
 ,即2x
,即2x ,解得x
,解得x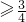 ,
,所以
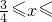 1;
1;③当x>1时,不等式可化为(x+1)-(x-1)
 ,即2
,即2 ,
,所以x>1;
综上,x
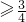 ,即不等式f(|x+1|-|x-1|)
,即不等式f(|x+1|-|x-1|) 的x的取值范围为x
的x的取值范围为x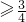 .
.分析:(1)先由f(x)求得g(x),进而得到y=g(x2-2x-3),根据复合函数单调性的判断方法可求得函数的单调增区间,注意函数的定义域;
(2)表示出不等式,利用指数函数的单调性可得|x+1|-|x-1|
 ,按照x≤-1,-1<x≤1,x>1三种情况讨论去掉绝对值符号即可解得不等式;
,按照x≤-1,-1<x≤1,x>1三种情况讨论去掉绝对值符号即可解得不等式;点评:本题考查复合函数的单调性、反函数以及绝对值不等式的求解,考查分类讨论思想,综合性较强,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目