题目内容
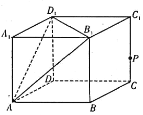
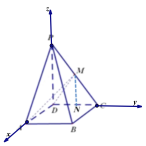
【题目】如图,在四棱锥![]() 中,四边形
中,四边形![]() 为正方形,
为正方形,![]() 平面
平面![]() ,点
,点![]() 是棱
是棱![]() 的中点,
的中点,![]() ,
,![]() .
.
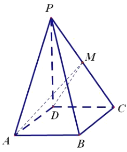
(1)若![]() ,证明:平面
,证明:平面![]() 平面
平面![]() ;
;
(2)若三棱锥![]() 的体积为
的体积为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)由已知可证得![]() 平面
平面![]() ,则有
,则有![]() ,在
,在![]() 中,由已知可得
中,由已知可得![]() ,即可证得
,即可证得![]() 平面
平面![]() ,进而证得结论.
,进而证得结论.
(2) 过![]() 作
作![]() 交
交![]() 于
于![]() ,由
,由![]() 为
为![]() 的中点,结合已知有
的中点,结合已知有![]() 平面
平面![]() .
.
则![]() ,可求得
,可求得![]() .建立坐标系分别求得面
.建立坐标系分别求得面![]() 的法向量
的法向量![]() ,平面
,平面![]() 的一个法向量为
的一个法向量为![]() ,利用公式即可求得结果.
,利用公式即可求得结果.
(1)证明:![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() ,又四边形
,又四边形![]() 为正方形,
为正方形,
![]() .
.
又![]() 、
、![]() 平面
平面![]() ,且
,且![]() ,
,
![]() 平面
平面![]() .
.![]() .
.
![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,
的中点,
![]() .
.
又![]() 、
、![]() 平面
平面![]() ,
,![]() ,
,
![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() .
.
(2)解:过![]() 作
作![]() 交
交![]() 于
于![]() ,如图
,如图
![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
![]() ,
,![]() .
.
所以![]() ,又
,又![]() 、
、![]() 、
、![]() 两两互相垂直,以
两两互相垂直,以![]() 、
、![]() 、
、![]() 为坐标轴建立如图所示的空间直角坐标系.
为坐标轴建立如图所示的空间直角坐标系.![]() ,
,![]() ,
,![]() ,
,![]()
设平面![]() 的法向量
的法向量![]() ,则
,则
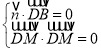 ,即
,即![]() .
.
令![]() ,则
,则![]() ,
,![]() .
.![]() .
.
![]() 平面
平面![]() 的一个法向量为
的一个法向量为![]()
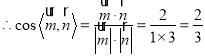 .
.
![]() 二面角
二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
【题目】每年9月第三周是国家网络安全宣传周.某学校为调查本校学生对网络安全知识的了解情况,组织了《网络信息辨析测试》活动,并随机抽取50人的测试成绩绘制了频率分布直方图如图所示:

(1)某学生的测试成绩是75分,你觉得该同学的测试成绩低不低?说明理由;
(2)将成绩在![]() 内定义为“合格”;成绩在
内定义为“合格”;成绩在![]() 内定义为“不合格”.①请将下面的
内定义为“不合格”.①请将下面的![]() 列联表补充完整; ②是否有90%的把认为网络安全知识的掌握情况与性别有关?说明你的理由;
列联表补充完整; ②是否有90%的把认为网络安全知识的掌握情况与性别有关?说明你的理由;
合格 | 不合格 | 合计 | |
男生 | 26 | ||
女生 | 6 | ||
合计 |
(3)在(2)的前提下,对50人按是否合格,利用分层抽样的方法抽取5人,再从5人中随机抽取2人,求恰好2人都合格的概率.附:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.65 | 10.828 |
![]() .
.