题目内容
已知O为坐标原点,直线l经过点P(2,0),且与抛物线y2=4x交于A、B两个不同点.(1)求证:直线OA与直线OB不垂直;
(2)如果点E(8,0)在以线段AB为直径的圆上,求直线l的方程.
答案:(1)证明:设A(x1,y1),B(x2,y2),则y12=4x1,y22=4x2,
![]() =(x1-2,y1),
=(x1-2,y1),![]() =(x2-2,y2),∵P、A、B共线,∴
=(x2-2,y2),∵P、A、B共线,∴![]() ∥
∥![]() .
.
∴(x1-2)y2-y1(x2-2)=0.由y12=4x1,y22=4x2得x1=![]() ,x2=
,x2=![]() ,
,
代入(x1-2)y2-y1(x2-2)=0,化简得y1y2=-8.
∵![]() =(x1,y1),
=(x1,y1),![]() =(x2,y2),∴x1x2+y1y2=
=(x2,y2),∴x1x2+y1y2=![]() +y1y2=-4≠0.
+y1y2=-4≠0.
∴![]() 与
与![]() 不垂直.∴直线OA与直线OB不垂直.
不垂直.∴直线OA与直线OB不垂直.
(2)解:∵![]() =(x1-8,y1),
=(x1-8,y1),![]() =(x2-8,y2),由点E(8,0)在以线段AB为直径的圆上得
=(x2-8,y2),由点E(8,0)在以线段AB为直径的圆上得![]() ⊥
⊥![]() .
.
∴(x1-8)(x2-8)+y1y2=0.
将x1=![]() ,x2=
,x2=![]() ,y1y2=-8代入(x1-8)(x2-8)+y1y2=0.∴y12+y22=30.
,y1y2=-8代入(x1-8)(x2-8)+y1y2=0.∴y12+y22=30.
∴y1+y2=±![]() =±
=±![]() .
.
∴直线AB的斜率存在,设其为k,则k=![]() =±
=±![]() .
.
∴直线AB的方程为y=±![]() (x-2).
(x-2).
∴当点E(8,0)在以线段AB为直径的圆上时,直线l的方程为y=±![]() (x-2).
(x-2).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
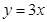 ,边AB所在的直
,边AB所在的直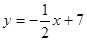 ,且顶点B的横坐标为6。
,且顶点B的横坐标为6。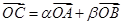 ,其中
,其中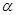
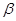 ∈R且
∈R且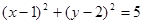 B.3x+2y-11=0 C.2x-y=0 D.x+2y=5
B.3x+2y-11=0 C.2x-y=0 D.x+2y=5