题目内容
在四边形ABCD中,“∃λ∈R,使得AB=λDC,AD=λBC”是“四边形ABCD为平行四边形”的( )
|
| A. | 充分而不必要条件 | B. | 必要而不充分条件 |
|
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
考点:
必要条件、充分条件与充要条件的判断.
专题:
证明题.
分析:
根据平行四边形的判定定理:两组对边分别平行的四边形是平行四边形和必要条件、充分条件与充要条件的定义进行判断即可.
解答:
解:由在四边形ABCD中,“∃λ∈R,使得AB=λDC,AD=λBC”,不能得出AB∥DC,AD∥BC,
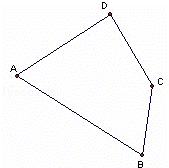
如图,AB=2DC,AD=2BC,不得到四边形ABCD为平行四边形.
也就不得到四边形ABCD为平行四边形,
反之,由四边形ABCD为平行四边形,得到AB=DC,AD=BC,从而有:∃λ=1∈R,使得AB=λDC,AD=λBC,
故在四边形ABCD中,“∃λ∈R,使得AB=λDC,AD=λBC”是“四边形ABCD为平行四边形”的必要而不充分条件.
故选B.
点评:
本题主要考查对平行四边形的判定定理,必要条件、充分条件与充要条件的判断,能灵活运用平行四边形的判定进行证明是解此题的关键,此题是一个比较综合的题目.

练习册系列答案
相关题目
 如图所示,在四边形ABCD中,EF∥BC,FG∥AD,则
如图所示,在四边形ABCD中,EF∥BC,FG∥AD,则