题目内容
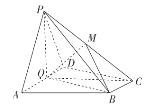
【题目】如图,三棱柱![]() 中,侧面
中,侧面![]() 是菱形,其对角线的交点为
是菱形,其对角线的交点为![]() ,且
,且![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)设![]() ,若直线
,若直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的正弦值.
的正弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)根据菱形的特征和题中条件得到![]() 平面
平面![]() ,结合线面垂直的定义和判定定理即可证明;
,结合线面垂直的定义和判定定理即可证明;![]() 2
2![]() 建立空间直角坐标系,利用向量知识求解即可.
建立空间直角坐标系,利用向量知识求解即可.
(1)证明:∵四边形![]() 是菱形,
是菱形,
![]() ,
,
![]()
![]() 平面
平面![]()
![]() 平面
平面![]() ,
,
![]()
又![]() 是
是![]() 的中点,
的中点,
![]() ,
,
又![]()
![]() 平面
平面![]()
(2)![]()
∴直线![]() 与平面
与平面![]() 所成的角等于直线
所成的角等于直线![]() 与平面
与平面![]() 所成的角.
所成的角.
![]() 平面
平面![]() ,
,
∴直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,即
,即![]() .
.
因为![]() ,则在等腰直角三角形
,则在等腰直角三角形![]() 中
中![]() ,
,
所以![]() .
.
在![]() 中,由
中,由![]() 得
得![]() ,
,
以![]() 为原点,分别以
为原点,分别以![]() 为
为![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() .
.
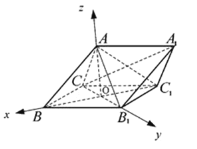
则![]()
所以![]()
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则 ,可得
,可得![]() ,
,
取平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则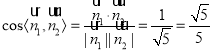 ,
,
所以二面角![]() 的正弦值的大小为
的正弦值的大小为![]() .
.
(注:问题(2)可以转化为求二面角![]() 的正弦值,求出
的正弦值,求出![]() 后,在
后,在![]() 中,过点
中,过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,连接
,连接![]() ,则
,则![]() 就是所求二面角平面角的补角,先求出
就是所求二面角平面角的补角,先求出![]() ,再求出
,再求出![]() ,最后在
,最后在![]() 中求出
中求出![]() .)
.)

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案【题目】自2017年起,部分省、市陆续实施了新高考,某省采用了“![]() ”的选科模式,即:考试除必考的语、数、外三科外,再从物理、化学、生物、历史、地理、政治六个学科中,任意选取三科参加高考,为了调查新高考中考生的选科情况,某地区调查小组进行了一次调查,研究考生选择化学与选择物理是否有关.已知在调查数据中,选物理的考生与不选物理的考生人数相同,其中选物理且选化学的人数占选物理人数的
”的选科模式,即:考试除必考的语、数、外三科外,再从物理、化学、生物、历史、地理、政治六个学科中,任意选取三科参加高考,为了调查新高考中考生的选科情况,某地区调查小组进行了一次调查,研究考生选择化学与选择物理是否有关.已知在调查数据中,选物理的考生与不选物理的考生人数相同,其中选物理且选化学的人数占选物理人数的![]() ,在不选物理的考生中,选化学与不选化学的人数比为
,在不选物理的考生中,选化学与不选化学的人数比为![]() .
.
(1)若在此次调查中,选物理未选化学的考生有100人,试完成下面的列联表:
选化学 | 不选化学 | 合计(人数) | |
选物理 | |||
不选物理 | |||
合计(人数) |
(2)根据第(1)问的数据,能否有99%把握认为选择化学与选择物理有关?
(3)若研究得到在犯错误概率不超过0.01的前提下,认为选化学与选物理有关,则选物理又选化学的人数至少有多少?(单位:千人;精确到0.001)
附: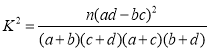 .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |