Question

21.已知（）是曲线上的点，，是数列的前项和，且满足，，….

（I）证明：数列（）是常数数列；

（II）确定的取值集合，使时，数列是单调递增数列；

（III）证明：当时，弦（）的斜率随单调递增.

 

Answer 1

解：（I）当时，由已知得.

因为，所以.    …… ①

于是.                                  ……②

由②－①得.                             …… ③

于是.                                 ……  ④

由④－③得，                                 …… ⑤

所以，即数列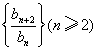是常数数列.

（II）由①有，所以.由③有，，所以，.

而⑤表明：数列和分别是以，为首项，6为公差的等差数列，

所以，，，

数列是单调递增数列且对任意的成立.

且

.

即所求的取值集合是.

（III）解法一：弦的斜率为

任取，设函数，则.

记，则，

当时，，在上为增函数，

当时，，在上为减函数，

所以时，，从而，所以在和上都是增函数.

由（II）知，时，数列单调递增，

取，因为，所以.

取，因为，所以.

所以，即弦的斜率随单调递增.

解法二：设函数，同解法一得，在和上都是增函数，

所以，.

故，即弦的斜率随单调递增.