题目内容
在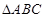 中,角
中,角 ,
, ,
, 的对边分别为
的对边分别为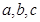 ,且
,且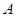 ,
,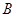 ,
,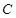 成等差数列.
成等差数列.
(1)若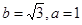 ,求
,求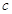 的值;(2)求sinA+sinC的最大值.
的值;(2)求sinA+sinC的最大值.
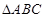 中,角
中,角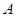 ,
,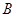 ,
,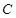 的对边分别为
的对边分别为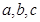 ,且
,且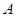 ,
,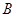 ,
,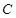 成等差数列.
成等差数列.(1)若
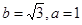 ,求
,求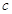 的值;(2)求sinA+sinC的最大值.
的值;(2)求sinA+sinC的最大值. (1)c=2(2)

本试题主要是考查了解三角形的运用。
(1)因为 成等差数列,
成等差数列,
所以 .故有
.故有 ,
,
则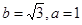 ,
, ,得到c的值,然后求解。
,得到c的值,然后求解。
(2)由已知sinA+sinC=sinA+sin( -B-A)=sinA+sin(
-B-A)=sinA+sin( -B)
-B)
=sinA+ cosA+
cosA+ sinA,结合三角函数的性质可知。
sinA,结合三角函数的性质可知。
解:(1)因为 成等差数列,
成等差数列,
所以 .
.
因为 ,
,
所以 . ………………………………2分
. ………………………………2分
法1: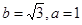 ,
, ,………………4分
,………………4分
所以 . …………………………6分
. …………………………6分
所以c=2或 (舍去). ……………………………7分
(舍去). ……………………………7分
法2:写出正弦定理 …………3分
…………3分
 ………………4分
………………4分

 ……………………………6分
……………………………6分
所以c=2……………………………7分(求出两种情形扣1分)
(2)解:由已知sinA+sinC=sinA+sin( -B-A)=sinA+sin(
-B-A)=sinA+sin( -B)……………10
-B)……………10
=sinA+ cosA+
cosA+ sinA………………12
sinA………………12
= sin(A+
sin(A+ )≤
)≤ .………13
.………13
当△ABC为正三角形时取等号。………………14
(1)因为
 成等差数列,
成等差数列,所以
 .故有
.故有 ,
,则
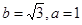 ,
, ,得到c的值,然后求解。
,得到c的值,然后求解。 (2)由已知sinA+sinC=sinA+sin(
 -B-A)=sinA+sin(
-B-A)=sinA+sin( -B)
-B)=sinA+
 cosA+
cosA+ sinA,结合三角函数的性质可知。
sinA,结合三角函数的性质可知。解:(1)因为
 成等差数列,
成等差数列,所以
 .
.因为
 ,
,所以
 . ………………………………2分
. ………………………………2分法1:
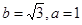 ,
, ,………………4分
,………………4分所以
 . …………………………6分
. …………………………6分所以c=2或
 (舍去). ……………………………7分
(舍去). ……………………………7分法2:写出正弦定理
 …………3分
…………3分 ………………4分
………………4分
 ……………………………6分
……………………………6分所以c=2……………………………7分(求出两种情形扣1分)
(2)解:由已知sinA+sinC=sinA+sin(
 -B-A)=sinA+sin(
-B-A)=sinA+sin( -B)……………10
-B)……………10=sinA+
 cosA+
cosA+ sinA………………12
sinA………………12=
 sin(A+
sin(A+ )≤
)≤ .………13
.………13 当△ABC为正三角形时取等号。………………14

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
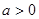 ,函数
,函数 ,
, 时,
时,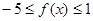 ,求常数
,求常数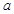 ,
,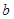 的值.
的值.  的一部分图象如图,那么
的一部分图象如图,那么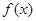 的解析式以及
的解析式以及
 的值分别是( )
的值分别是( )
 ,
, 
 ,
, 
 ,
,  ,
,  在抛物线
在抛物线 上,点
上,点 在圆
在圆 上,
上, 的最小值为( )
的最小值为( )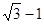



 为奇函数,该函数的部分图 像如图所示,
为奇函数,该函数的部分图 像如图所示,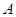 、
、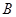 分别为最高点与最低点,且
分别为最高点与最低点,且
 ,则该函数图象的一条对称轴为( )
,则该函数图象的一条对称轴为( )




 ,设
,设 (Ⅰ)求函数
(Ⅰ)求函数 的内角
的内角 的对边分别为
的对边分别为 ,已知
,已知
 ,求边
,求边 的值.
的值. (
( )的图象如右图所示,为了得到
)的图象如右图所示,为了得到 的图象,可以将
的图象,可以将 的图象( )
的图象( )
 个单位长度
个单位长度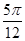 个单位长度
个单位长度 ,有下列命题:
,有下列命题: ,且
,且 ;
;  对称;
对称;  求得 。
求得 。 的图象,只要将函数
的图象,只要将函数 的图象( )
的图象( )  单位
单位 单位
单位