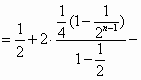题目内容
若数列{an}满足![]() -
-![]() =d,其中d为常数,则称数列{an}为等方差数列.已知等方差数列{an}满足an>0,a1=1,a1,a2,a5成等比数列且互不相等.
=d,其中d为常数,则称数列{an}为等方差数列.已知等方差数列{an}满足an>0,a1=1,a1,a2,a5成等比数列且互不相等.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列![]() 的前n项和;
的前n项和;
(Ⅲ)是否存在实数m,使得对一切正整数n,总有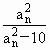 ≤m成立?若存在,求实数m的取值范围,若不存在,说明理由.
≤m成立?若存在,求实数m的取值范围,若不存在,说明理由.
答案:
解析:
解析:
|
(Ⅰ)由 即 数列 (Ⅱ) 设 ①-②,得 即数列 (Ⅲ)假设存在实数 即 设 当 故存在 |

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目