题目内容

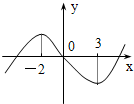
函数f（x）=x3+bx2+cx+d图象如图，则函数y=x2+
2
3
bx+
c
3
的单调递增区间为（　　）
A．（-∞，-2]B．[3，+∞）C．[-2，3]D．[
1
2
，+∞）
精英家教网
∵f（x）=x3+bx2+cx+d，∴f'（x）=3x2+2bx+c
由图可知f'（-2）=0，f'（3）=0
∴12-4b+c=0，27+6b+c=0，∴b=-1.5，c=-18
∴y=x2-x-6，y'=2x-1，当x＞
1
2
时，y'＞0
∴y=x2-x-6的单调递增区间为：[
1
2
，+∞）
故选D．
练习册系列答案
相关题目
已知函数f（x）=-x3+ax2+bx+c在（-∞，0）上是减函数，在（0，1）上是增函数，函数f（x）在R上有三个零点．
（1）求b的值；
（2）若1是其中一个零点，求f（2）的取值范围；
（3）若a=1，g（x）=f′（x）+3x2+lnx，试问过点（2，5）可作多少条直线与曲线y=g（x）相切？请说明理由．
（2007•东城区一模）已知函数f（x）=x3+ax2+bx+c，曲线y=f（x）在点x=1处的切线l不过第四象限且斜率为3，又坐标原点到切线l的距离为
10
10
，若x=
2
3
时，y=f（x）有极值．
（1）求a，b，c的值；
（2）求y=f（x）在[-3，1]上的最大值和最小值．
（2013•宁波模拟）已知函数f（x）=x3+ax2-a2x+2，a∈R．
（1）若a＜0时，试求函数y=f（x）的单调递减区间；
（2）若a=0，且曲线y=f（x）在点A、B（A、B不重合）处切线的交点位于直线x=2上，证明：A、B 两点的横坐标之和小于4；
（3）如果对于一切x1、x2、x3∈[0，1]，总存在以f（x1）、f（x2）、f（x3）为三边长的三角形，试求正实数a的取值范围．
设函数f（x）=x3-3ax+b（a≠0），已知曲线y=f（x）在点（2，f（x））处在直线y=8相切．
（Ⅰ）求a，b的值；
（Ⅱ）求函数f（x）的单调区间与极值点．
对于函数f（x）=x3+ax2-x+1的极值情况，4位同学有下列说法：甲：该函数必有2个极值；乙：该函数的极大值必大于1；丙：该函数的极小值必小于1；丁：方程f（x）=0一定有三个不等的实数根． 这四种说法中，正确的个数是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网