题目内容
(本小题满分14分)
已知函数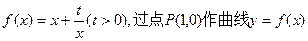 的两条切线PM、PN,切点分
的两条切线PM、PN,切点分 别为M、N.
别为M、N.
(I)当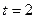 时,求函数
时,求函数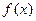 的单调
的单调 递增区间;
递增区间;
(II)设|MN|=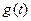 ,试求函数
,试求函数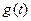 的表达式;
的表达式;
(III)在(II)的条件下,若对任意的正整数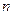 ,在区间
,在区间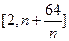 内,总存在m+1个数
内,总存在m+1个数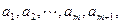 使得不等式
使得不等式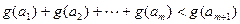 成立,求m的最大值.
成立,求m的最大值.
已知函数
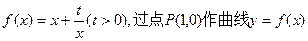 的两条切线PM、PN,切点分
的两条切线PM、PN,切点分 别为M、N.
别为M、N.(I)当
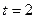 时,求函数
时,求函数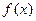 的单调
的单调 递增区间;
递增区间;(II)设|MN|=
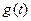 ,试求函数
,试求函数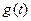 的表达式;
的表达式;(III)在(II)的条件下,若对任意的正整数
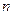 ,在区间
,在区间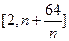 内,总存在m+1个数
内,总存在m+1个数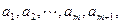 使得不等式
使得不等式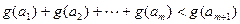 成立,求m的最大值.
成立,求m的最大值.(1) (2)
(2) (3)6
(3)6
 (2)
(2) (3)6
(3)6(I)当

 …………………1分
…………………1分
 .则函数
.则函数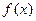 有单调递增区间为
有单调递增区间为 …2分
…2分
(II)设M、N两点的横坐标分别为 、
、 ,
,
 同理,由切线PN也过点(1,0),得
同理,由切线PN也过点(1,0),得 (2)
(2)
由(1)、(2),可得 的两根,
的两根,
 ……………………………………………………6分
……………………………………………………6分


把(*)式代入,得
因此,函数 ………………8分
………………8分
(III)易知 上为增函数,
上为增函数,

 …………10分
…………10分


由于m为正整数, .………………………………………………13分
.………………………………………………13分
 又当
又当
因此,m的最大值为6. ……………………………………………………14分


 …………………1分
…………………1分 .则函数
.则函数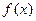 有单调递增区间为
有单调递增区间为 …2分
…2分(II)设M、N两点的横坐标分别为
 、
、 ,
,
|
 同理,由切线PN也过点(1,0),得
同理,由切线PN也过点(1,0),得 (2)
(2)由(1)、(2),可得
 的两根,
的两根, ……………………………………………………6分
……………………………………………………6分

把(*)式代入,得

因此,函数
 ………………8分
………………8分(III)易知
 上为增函数,
上为增函数,
 …………10分
…………10分

由于m为正整数,
 .………………………………………………13分
.………………………………………………13分 又当
又当
因此,m的最大值为6. ……………………………………………………14分

练习册系列答案
相关题目
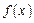 的定义域为R,当x<0时,
的定义域为R,当x<0时,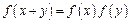 .
.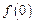 ,判断并证明函数
,判断并证明函数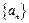 满足
满足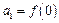 ,且
,且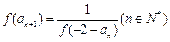 ,
,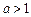 时,不等式
时,不等式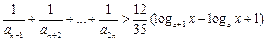 对不小于2的正整数
对不小于2的正整数
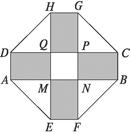
 构成的面积为
构成的面积为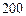
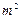 的十字型地域,计划在正方形
的十字型地域,计划在正方形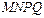 上建一座“观景花坛”,
上建一座“观景花坛”,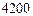 元/
元/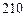 元/
元/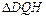 等)上铺草坪,造价为
等)上铺草坪,造价为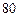 元/
元/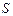 元,
元,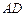 长为
长为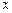
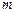 ,试建立
,试建立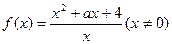 。
。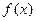 为奇函数,求
为奇函数,求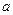 的值;
的值;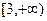 上恒大于0,求
上恒大于0,求
 的最大值
的最大值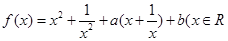 ,且
,且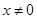 )若实数
)若实数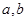 使得函数
使得函数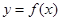 在定义域上有零点,则
在定义域上有零点,则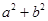 的最小值为__________.
的最小值为__________. 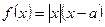
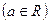 .
.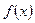 在
在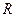 上的奇偶性;
上的奇偶性;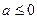 时,求函数
时,求函数 ]上的最大值.
]上的最大值.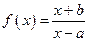 在
在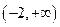 上是增函数的一个充分非必要条件是 .
上是增函数的一个充分非必要条件是 . 的最小值为 .
的最小值为 .