题目内容
已知函数f (x) =(2 -a )(x -1 )-2lnx ,(a ∈R ,e 为自然对数的底数)
(1 )当a =1 时,求f (x) 的单调区间;
(2 )若函数f (x) 在(0 ,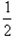 )上无零点,求a的最小值
)上无零点,求a的最小值
(1 )当a =1 时,求f (x) 的单调区间;
(2 )若函数f (x) 在(0 ,
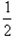 )上无零点,求a的最小值
)上无零点,求a的最小值解:(Ⅰ)当 a=1时,
由 由
由
故 的单调减区间为
的单调减区间为 单调增区间为
单调增区间为 
(Ⅱ)因为 在
在  上恒成立不可能,故要使函数
上恒成立不可能,故要使函数 在
在  上无零点,
上无零点,
只要对任意的 恒成立,即对
恒成立,即对 恒成立.
恒成立.
令 则
则 
再令
 在
在 上为减函数,
上为减函数,
于是
从而 , ,
, ,
于是 在
在  上为增函数 故要使
上为增函数 故要使 恒成立,
恒成立,
只要
综上,若函数 在
在  上无零点,则
上无零点,则  的最小值为
的最小值为

由
 由
由
故
 的单调减区间为
的单调减区间为 单调增区间为
单调增区间为 
(Ⅱ)因为
 在
在  上恒成立不可能,故要使函数
上恒成立不可能,故要使函数 在
在  上无零点,
上无零点,只要对任意的
 恒成立,即对
恒成立,即对 恒成立.
恒成立.令
 则
则 
再令

 在
在 上为减函数,
上为减函数,于是

从而
 , ,
, ,于是
 在
在  上为增函数 故要使
上为增函数 故要使 恒成立,
恒成立,只要

综上,若函数
 在
在  上无零点,则
上无零点,则  的最小值为
的最小值为

练习册系列答案
相关题目
 已知函数f(x)=
已知函数f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|