题目内容
已知 是R上的奇函数,
是R上的奇函数, +f(1)(n∈N*),若
+f(1)(n∈N*),若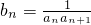 ,记{bn}的前n项和为Sn,则
,记{bn}的前n项和为Sn,则 =________.
=________.

分析:根据
 是R上的奇函数,可得
是R上的奇函数,可得 +
+ =4,由
=4,由 +f(1),倒序相加,可得an=2(n+1),从而可得
+f(1),倒序相加,可得an=2(n+1),从而可得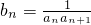 =
= (
( ),叠加,即可求得数列的和,从而可求极限.
),叠加,即可求得数列的和,从而可求极限.解答:∵
 是R上的奇函数,
是R上的奇函数,∴F(-x)=-F(x)
∴
 +
+ =4
=4∴函数f(x)关于点(
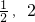 )对称
)对称∵
 +f(1)
+f(1)∴2an=4(n+1)
∴an=2(n+1)
∴
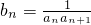 =
= (
( )
)∴{bn}的前n项和为Sn=
 )=
)=
∴
 =
=
故答案为:

点评:本题考查函数的性质,考查数列的通项与求和,考查数列的极限,确定数列的通项是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 是R上的奇函数
是R上的奇函数
 .
. 是R上的奇函数,则a =
是R上的奇函数,则a =  是R上的奇函数且在
是R上的奇函数且在 上单调递增,令
上单调递增,令 ,
, 则 ( )
则 ( ) B.
B.
 D.
D.
 是R上的奇函数,
是R上的奇函数,


 ,则数列
,则数列 的通项公式为 ( )
的通项公式为 ( ) B.
B. C.
C. D.
D.