题目内容
设 、
、 、
、 是同一平面的三个单位向量,且
是同一平面的三个单位向量,且 , 则
, 则 的最小值为( )
的最小值为( )
| A.-1 | B.-2 | C.1- | D. |
C
解析试题分析:根据题意,由于 、
、 、
、 是同一平面的三个单位向量,则其模长为1,那么由于
是同一平面的三个单位向量,则其模长为1,那么由于 ,那么借助于二次函数的性质可知,最小值为1-
,那么借助于二次函数的性质可知,最小值为1- ,故选C.
,故选C.
考点:向量的数量积
点评:解决的关键是利用向量的数量积的公示的 准确表示,并借助于函数来得到最值,属于基础题。

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
已知点 ,点
,点 ,向量
,向量 ,若
,若 ,则实数
,则实数 的值为( )
的值为( )
| A.5 | B.6 | C.7 | D.8 |
已知 ,
, 与
与 的夹角为
的夹角为 ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
已知点G是ΔABC的重心, ,
,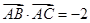 ,则
,则 的最小值是
的最小值是
A.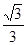 | B. | C. | D. |
设平面向量 ,
, ,若向量
,若向量 共线,则
共线,则 =( )
=( )
A. | B. | C. | D. |
已知O是坐标原点, ,若点
,若点 为平面区域
为平面区域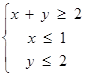 上一动点,则
上一动点,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
 的函数
的函数 图像的两个端点为
图像的两个端点为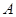 、
、 ,
, 是
是 .已知向量
.已知向量 ,若不等式
,若不等式 恒成立,则称函数
恒成立,则称函数 阶线性近似”.若函数
阶线性近似”.若函数 在
在 上“
上“

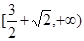

 等于( )
等于( ) B.
B. C.
C.  D.
D. 
 =2
=2 ,
, =
= ,则
,则 =
=