题目内容
已知AB是⊙O的直径，BC是⊙O的切线，切点为B，OC平行于弦AD.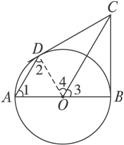
图2-3-8
求证：DC是⊙O的切线.
思路分析:要证DC是⊙O的切线，因为D是圆上的点，所以应想到连结OD，再证明OD与DC垂直即可.题目中已经有∠OBC是直角，根据图形，考虑证明三角形全等.
证明:连结OD.∵OA=OD，
∴∠1=∠2.
∵AD∥OC，∴∠1=∠3,∠2=∠4.
∴∠3=∠4.
在△OBC和△ODC中，OB=OD，∠3=∠4，OC=OC，
∴△OBC≌△ODC.
∴∠OBC=∠ODC.
∵BC是⊙O的切线，∴∠OBC=90°.
∴∠ODC=90°.
∴DC是⊙O的切线.
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
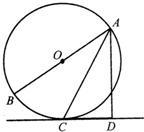如图，已知AB是⊙O的直径，AC为弦，且平分∠BAD，AD⊥CD，垂足为D．
如图，已知AB是⊙O的直径，AC是弦，AD⊥CE，垂足为D，AC平分∠BAD．
如图，已知AB是⊙O的直径，AB⊥CD于E，切线BF交AD的延长线于F，若AB=10，CD=8，则切线BF的长是
如图，已知AB是⊙O的直径，点C是⊙O上的动点（异于A、B），过动点C的直线VC垂直于⊙O所在的平面，D，E分别是VA，VC的中点．
如图，已知AB是⊙O的直径，⊙O的切线PA与弦BC的延长线相交于点P，∠PBA的平分线交PA于点D，∠ABC=30°．