题目内容
已知函数f(x)=ln(1+x)-x+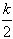 x2(k≥0)。
x2(k≥0)。
(1)当k=2时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)求f(x)的单调区间。
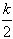 x2(k≥0)。
x2(k≥0)。(1)当k=2时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)求f(x)的单调区间。
解:(1)当k=2时,f(x)=ln(1+x)-x+x2,f'(x)=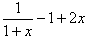
由于f(1)=ln2,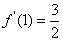
所以曲线y=f(x)在点(1,f(1))处的切线方程为
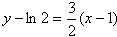
即3x-2y+21n2-3=0;
(2)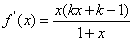 ,
,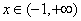
当k=0时,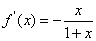
所以,在区间(-1,0)上,f'(x)>0;
在区间(0,+∞)上,f'(x)<0
故f(x)的单调递增区间是(-1,0),单调递减区间是(0,+∞)
当0<k<1时,由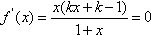
得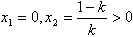
所以,在区间(-1,0)和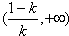 上,f'(x)>0;
上,f'(x)>0;
在区间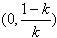 上,f'(x)<0
上,f'(x)<0
故f(x)的单调递增区间是(-1,0)和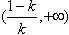 ,单调递减区间是
,单调递减区间是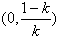
当k=1时,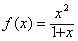
故f(x)的单调递增区间是(-1,+∞)
当k>1时,由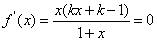
得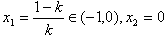
所以,在区间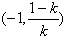 和(0,+∞)上,f'(x)>0
和(0,+∞)上,f'(x)>0
在区间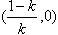 上,f'(x)<0
上,f'(x)<0
故f(x)的单调递增区间是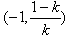 和(0,+∞)
和(0,+∞)
单调递减区间是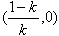 。
。
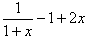
由于f(1)=ln2,
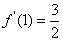
所以曲线y=f(x)在点(1,f(1))处的切线方程为
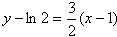
即3x-2y+21n2-3=0;
(2)
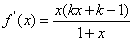 ,
,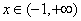
当k=0时,
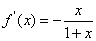
所以,在区间(-1,0)上,f'(x)>0;
在区间(0,+∞)上,f'(x)<0
故f(x)的单调递增区间是(-1,0),单调递减区间是(0,+∞)
当0<k<1时,由
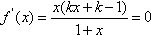
得
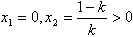
所以,在区间(-1,0)和
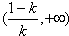 上,f'(x)>0;
上,f'(x)>0;在区间
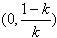 上,f'(x)<0
上,f'(x)<0故f(x)的单调递增区间是(-1,0)和
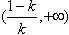 ,单调递减区间是
,单调递减区间是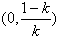
当k=1时,
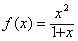
故f(x)的单调递增区间是(-1,+∞)
当k>1时,由
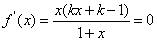
得
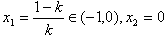
所以,在区间
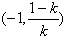 和(0,+∞)上,f'(x)>0
和(0,+∞)上,f'(x)>0在区间
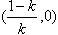 上,f'(x)<0
上,f'(x)<0故f(x)的单调递增区间是
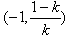 和(0,+∞)
和(0,+∞)单调递减区间是
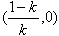 。
。
练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目