题目内容
已知数列{an}满足a1=22,an+1-an=2n,则数列{an}的通项公式为________, 的最小值为________.
的最小值为________.
an=n2-n+22 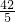
分析:先对数列的递推关系式进行转化即an=an-1+2(n-1)=[an-2+2(n-2)]+2(n-1)=an-3+2(n-3)+2(n-2)+2(n-1)=…,一步步向前推即可求出数列{an}的通项公式;再利用求出的数列{an}的通项公式,直接代入 利用基本不等式即可求
利用基本不等式即可求 的最小值.(注意n为正整数).
的最小值.(注意n为正整数).
解答:由an+1-an=2n得,
an=an-1+2(n-1)
=[an-2+2(n-2)]+2(n-1)
=an-3+2(n-3)+2(n-2)+2(n-1)
=…
=a1+2×1+2×2+…+2(n-1)
=22+2×
=n2-n+22.
所以 =n+
=n+ -1
-1
≥2 -1,等号成立时n=
-1,等号成立时n= ?n=
?n= ,
,
又因为n为正整数,故n=5,
此时 =5+
=5+ -1=
-1=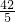 .
.
故答案为:n2-n+22,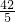 .
.
点评:本题主要考查数列的递推关系式的应用和等差数列的求和公式以及基本不等式的应用问题.知识点较多,但都是基础知识,属于中档题目.本题的易错点在于n为正整数这一限制条件的应用.
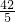
分析:先对数列的递推关系式进行转化即an=an-1+2(n-1)=[an-2+2(n-2)]+2(n-1)=an-3+2(n-3)+2(n-2)+2(n-1)=…,一步步向前推即可求出数列{an}的通项公式;再利用求出的数列{an}的通项公式,直接代入
 利用基本不等式即可求
利用基本不等式即可求 的最小值.(注意n为正整数).
的最小值.(注意n为正整数).解答:由an+1-an=2n得,
an=an-1+2(n-1)
=[an-2+2(n-2)]+2(n-1)
=an-3+2(n-3)+2(n-2)+2(n-1)
=…
=a1+2×1+2×2+…+2(n-1)
=22+2×

=n2-n+22.
所以
 =n+
=n+ -1
-1≥2
 -1,等号成立时n=
-1,等号成立时n= ?n=
?n= ,
,又因为n为正整数,故n=5,
此时
 =5+
=5+ -1=
-1=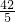 .
.故答案为:n2-n+22,
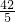 .
.点评:本题主要考查数列的递推关系式的应用和等差数列的求和公式以及基本不等式的应用问题.知识点较多,但都是基础知识,属于中档题目.本题的易错点在于n为正整数这一限制条件的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目